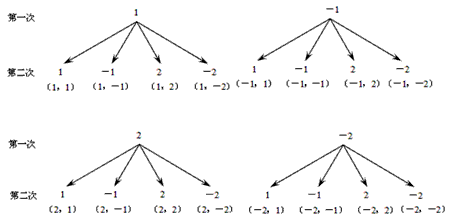
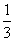六张大小、质地均相同的卡片上分别标有1、2、3、4、5、6,现将标有数字的一面朝下扣在桌面上,从中随机抽取一张(放回洗匀),再随机抽取第二张.(1)用列表法或树状图表示出前后-九年级数学
题文
| 六张大小、质地均相同的卡片上分别标有1、2、3、4、5、6,现将标有数字的一面朝下扣在桌面上,从中随机抽取一张(放回洗匀),再随机抽取第二张. (1)用列表法或树状图表示出前后两次抽得的卡片上所标数字的所有可能结果; (2)记前后两次抽得的数字分别为m、n,若把m、n分别作为点A的横坐标和纵坐标,求点  在函数 在函数 的图象上的概率. 的图象上的概率. |
答案
(1)树状图: 从树状图可以看出,所有可能出现的结果有36种,即: (1,1)、(1、2)、(1、3)、(1、4)、(1、5)、(1、6)、(2,1)、(2、2)、(2、3)、(2、4)、(2、5)、(2、6)(3,1)、(3、2)、(3、3)、(3、4)、(3、5)、(3、6)(4,1)、(4、2)、(4、3)、(4、4)、(4、5)、(4、6)(5,1)、(5、2)、(5、3)、(5、4)、(5、5)、(5、6)(6,1)、(6、2)、(6、3)、(6、4)、(6、5)、(6、6) (2)有4个点(2,6)、(3,4)、(4,3)、(6,2)在函数  的图象上 的图象上 所求概率  |
据专家权威分析,试题“六张大小、质地均相同的卡片上分别标有1、2、3、4、5、6,现将标..”主要考查你对 列举法求概率,求反比例函数的解析式及反比例函数的应用,利用概率解决问题 等考点的理解。关于这些考点的“档案”如下:
列举法求概率求反比例函数的解析式及反比例函数的应用利用概率解决问题
考点名称:列举法求概率
- 可能条件下概率的意义:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=
 。
。
等可能条件下概率的特征:
(1)对于每一次试验中所有可能出现的结果都是有限的;
(2)每一个结果出现的可能性相等。 - 概率的计算方法:
(1)列举法(列表或画树状图),
(2)公式法;
列表法或树状图这两种举例法,都可以帮助我们不重不漏的列出所以可能的结果。
列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
(2)列表法的应用场合
当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法。
(2)运用树状图法求概率的条件
当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
考点名称:求反比例函数的解析式及反比例函数的应用
反比例函数解析式的确定方法:
由于在反比例函数关系式 :y= 中,只有一个待定系数k,确定了k的值,也就确定了反比例函数。因此,只需给出一组x、y的对应值或图象上一点的坐标,代入
中,只有一个待定系数k,确定了k的值,也就确定了反比例函数。因此,只需给出一组x、y的对应值或图象上一点的坐标,代入 中即可求出k的值,从而确定反比例函数的关系式。但在实际求反比例函数的解析式时,应该具体问题具体分析。
中即可求出k的值,从而确定反比例函数的关系式。但在实际求反比例函数的解析式时,应该具体问题具体分析。反比例函数的应用:
建立函数模型,解决实际问题。- 用待定系数法求反比例函数关系式的一般步骤是:
①设所求的反比例函数为:y= (k≠0);
(k≠0);
②根据已知条件(自变量与函数的对应值)列出含k的方程;
③由代人法解待定系数k的值;
④把k值代人函数关系式y= 中。
中。
反比例函数应用一般步骤:
①审题;
②求出反比例函数的关系式;
③求出问题的答案,作答。
考点名称:利用概率解决问题
- 应用概率可以解决以下问题:
(1)彩票中奖率的问题;
(2)抽样检测中产品合格率的问题;
(3)天气预报降水的概率;
(4)抛硬币、掷骰字的问题;
(5)圆盘分几个区域,分别涂色,转到哪个颜色的区域的概率;
(6)有刚回及无放回的摸球问题。
概率的应用情况远不止于这些,还有很多类似情况,在解决这类问题时,要充分理解题意,找到切入点,就能轻松的解决问题。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球-九年级数学
下一篇:“五·一”假期,梅河公司组织部分员工到A、B、C三地旅游,公司购买前往各地的车票种类、数量绘制成条形统计图,如图.根据统计图回答下列问题:(1)前往A地的车票有_____张,前往-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

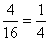
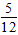
![有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是[]A、B、C、D、-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/114/2019-05-19/1f98957f1a502bb89c7421e326170484.gif)