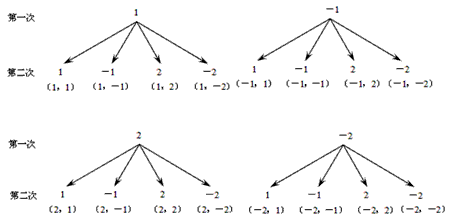
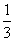如图,两个转盘A,B都被分成了3个全等的扇形,在每一个扇形内均标有不同的自然数,固定指针,同时转动转盘A,B,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形-数学
题文
| 如图,两个转盘A,B都被分成了3个全等的扇形,在每一个扇形内均标有不同的自然数,固定指针,同时转动转盘A,B,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形) (1)用列表法(或树形图)表示两个转盘停止转动后指针所指扇形内的数字的所有可能结果; (2)小明每转动一次就记录数据,并算出两数之和,其中“和为7”的频数及频率如下表:
(3)根据(2),若0<x<y,试求出x与y的值. 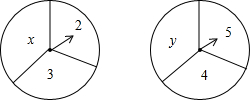 |

 。
。 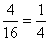
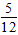
![有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是[]A、B、C、D、-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/114/2019-05-19/1f98957f1a502bb89c7421e326170484.gif)