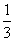小明、小华两人各自投掷一个质地均匀的正方体骰子,观察向上一面的点数.(1)求两个骰子点数的和是9的概率;(2)小明、小华约定:如果两者之积为奇数,那么小明得1分.如果两者之-数学
题文
| 小明、小华两人各自投掷一个质地均匀的正方体骰子,观察向上一面的点数. (1)求两个骰子点数的和是9的概率; (2)小明、小华约定:如果两者之积为奇数,那么小明得1分.如果两者之积为偶数,那么小华得1分.连续投掷20次,谁得分高,谁就获奖.你认为这个游戏公平吗?如果不公平,请为他们设计一个公平的游戏. |
答案
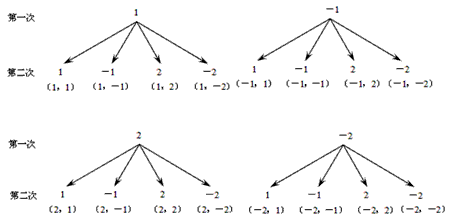
不妨把两个骰子分别记为第1个和第2个,列出下表:
(1)满足两个骰子点数的和是9(记为事件A)的结果有4个, 所以P(A)=
(2)不公平.(5分) 因为满足积为奇数(记为事件B)的结果有9个,积为偶数(记为事件C)的结果有27个, 所以P(B)=
所以P(B)>P(C),即小明得分机会大于小华得分机会.(8分) 改为:如果两者之积为奇数,那么小明得(3分), 如果两者之积为偶数,那么小华得(1分). 连续投掷20次,谁得分高,谁就获奖.(10分) |
据专家权威分析,试题“小明、小华两人各自投掷一个质地均匀的正方体骰子,观察向上一面..”主要考查你对 列举法求概率,利用概率解决问题 等考点的理解。关于这些考点的“档案”如下:
列举法求概率利用概率解决问题
考点名称:列举法求概率
- 可能条件下概率的意义:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=
 。
。
等可能条件下概率的特征:
(1)对于每一次试验中所有可能出现的结果都是有限的;
(2)每一个结果出现的可能性相等。 - 概率的计算方法:
(1)列举法(列表或画树状图),
(2)公式法;
列表法或树状图这两种举例法,都可以帮助我们不重不漏的列出所以可能的结果。
列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
(2)列表法的应用场合
当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法。
(2)运用树状图法求概率的条件
当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
考点名称:利用概率解决问题
- 应用概率可以解决以下问题:
(1)彩票中奖率的问题;
(2)抽样检测中产品合格率的问题;
(3)天气预报降水的概率;
(4)抛硬币、掷骰字的问题;
(5)圆盘分几个区域,分别涂色,转到哪个颜色的区域的概率;
(6)有刚回及无放回的摸球问题。
概率的应用情况远不止于这些,还有很多类似情况,在解决这类问题时,要充分理解题意,找到切入点,就能轻松的解决问题。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:在两个袋子中分别装有大小、质地完全相同的卡片.甲袋中放了3张卡片,卡片上的数字分别为1,2,3;乙袋中放了2张卡片,卡片上的数字分别为4,5.张红和李欣两人做游戏,分别从-数学
下一篇:丁丁与聪聪在一起做游戏,用“石头剪子布”的方法确定游戏的先后顺序,问在一回合中两个人都出“布”的概率是______.-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

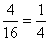
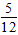
![有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是[]A、B、C、D、-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/114/2019-05-19/1f98957f1a502bb89c7421e326170484.gif)