某厂拟生产一种八年级学生使用的文具,但无法确定其颜色。为此,就该文具的颜色,小亮调查了八(1)班50位同学,结果如下:红、红、黄、绿、蓝、红、黄、红、红、绿、黄、红、红-八年级数学
题文
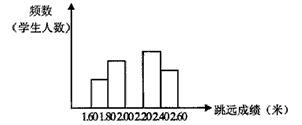
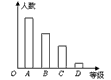
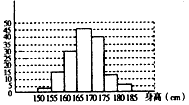
| 某厂拟生产一种八年级学生使用的文具,但无法确定其颜色。为此,就该文具的颜色,小亮调查了八(1)班50位同学,结果如下:红、红、黄、绿、蓝、红、黄、红、红、绿、黄、红、红、绿、黄、绿、红、红、黄、绿、红、红、黄、红、绿、蓝、红、红、绿、蓝、黄、红、绿、蓝、红、红、红、绿、蓝、红、绿、黄、红、红、绿、绿、蓝、红、红、绿。 (1)根据上面结果,你能很快说出该班同学最喜欢哪种颜色的文具吗? (2)你认为小亮的数据表示方式好不好?你能设计出一个比较好的表示方式吗? (3)小丽根据小亮的结果制成了下面两个图表,你能从中迅速判断出该班同学最喜欢哪种颜色的文具吗?该班同学所喜欢的四种颜色的频数、频率分别是多少? |
  |
| (4)你认为小亮的调查反映了所有八年级同学对这种文具颜色的喜好情况吗? (5)为了更为准确地为文具厂商提供信息,你认为抽样调查时应注意什么? (6)该文具厂就该种文具的颜色随机地调查了5000名八年级同学,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制了下面的图。随着调查次数的增加,红色的频率是如何变化的?你能估计调查到10000名同学时,红色的频率是多少吗? (7)你认为该厂在生产该种文具时,对文具的颜色应如何安排? |
 |
答案
| 解:(1)“略”; (2)小亮的数据表示方式较为杂乱,一般难以很快说出该班同学最喜欢哪种颜色的文具; (3)小丽的两个图表较为清晰,可以从中迅速判断出该班同学最喜欢哪种颜色的文具,该班同学所喜欢的红、黄、绿、蓝四种颜色的频数分别是23,8,13,6,频率分别是46%,16%,26%,12%; (4)小亮的调查不能反映所有八年级同学对这种文具颜色的喜好情况; (5)为了更为准确地为文具厂商提供信息,抽样调查时应再进行更广泛更随机的抽样调查; (6)随着调查次数的增加,红色的频率基本稳定在40%左右,因此可以估计调查到10000名同学时,红色的频率仍大约是40%左右; (7)该厂在生产该种文具时,一般可安排生产40%左右红色文具,20%左右绿色文具,18%左右黄色文具,12%左右蓝色文具,10%左右其他颜色文具。 |
据专家权威分析,试题“某厂拟生产一种八年级学生使用的文具,但无法确定其颜色。为此,..”主要考查你对 直方图,全面调查和抽样调查 ,频数与频率,折线图 等考点的理解。关于这些考点的“档案”如下:
直方图全面调查和抽样调查 频数与频率折线图
考点名称:直方图
- 频数分布直方图的定义:
在统计数据时,按照频数分布表,在平面直角坐标系中,横轴标出每个组的端点,纵轴表示频数,每个矩形的高代表对应的频数,称这样的统计图为频数分布直方图。
相关概念:
组数:在统计数据时,我们把数据按照不同的范围分成几个组,分成的组的个数称为组数。
组距:每一组两个端点的差。 频数分布直方图的特点:
①能够显示各组频数分布的情况;
②易于显示各组之间频数的差别。作直方图的目的有:
作直方图的目的就是通过观察图的形状,判断生产过程是否稳定,预测生产过程的质量。
1判断一批已加工完毕的产品;
搜集有关数据。
直方图将数据根据差异进行分类,特点是明察秋毫地掌握差异。
2在公路工程质量管理中,作直方图的目的有:
①估算可能出现的不合格率;
②考察工序能力估算法
③判断质量分布状态;
④判断施工能力;- 直方图绘制注意事项:
a. 抽取的样本数量过小,将会产生较大误差,可信度低,也就失去了统计的意义。因此,样本数不应少于50个。
b. 组数 k 选用不当,k 偏大或偏小,都会造成对分布状态的判断有误。
c. 直方图一般适用于计量值数据,但在某些情况下也适用于计数值数据,这要看绘制直方图的目的而定。
d. 图形不完整,标注不齐全,直方图上应标注:公差范围线、平均值 的位置(点画线表示)不能与公差中心M相混淆;图的右上角标出:N、S、C p或 CPK. 制作频数分布直方图的方法:
①集中和记录数据,求出其最大值和最小值。数据的数量应在100个以上,在数量不多的情况下,至少也应在50个以上。 我们把分成组的个数称为组数,每一个组的两个端点的差称为组距。
②将数据分成若干组,并做好记号。分组的数量在5-12之间较为适宜。
③计算组距的宽度。用最大值和最小值之差去除组数,求出组距的宽度。
④计算各组的界限位。各组的界限位可以从第一组开始依次计算,第一组的下界为最小值减去最小测定单位的一半,第一组的上界为其下界值加上组距。第二组的下界限位为第一组的上界限值,第二组的下界限值加上组距,就是第二组的上界限位,依此类推。
⑤统计各组数据出现频数,作频数分布表。
⑥作直方图。以组距为底长,以频数为高,作各组的矩形图。应用步骤:
(1)收集数据。作直方图的数据一般应大于50个。
(2)确定数据的极差(R)。用数据的最大值减去最小值 求得。
(3)确定组距(h)。先确定直方图的组数,然后以此组数去除极差,可得直方图每组的宽度,即组距。组数的确定要适当。组数太少,会引起较大计算误差;组数太多,会影响数据分组规律的明显性,且计算工作量加大。
(4)确定各组的界限值。为避免出现数据值与组界限值重合而造成频数据计算困难,组的界限值单位应取最小测量单位的1/2。分组时应把数据表中最大值和最小值包括在内。
第一组下限值为:最小值-0.5;
第一组上限值为:第一组下限值加组距;
第二组下限值就是第一组的上限值;
第二组上限值就是第二组的下限值加组距;
第三组以后,依此类推定出各组的组界。
(5)编制频数分布表。把多个组上下界限值分别填入频数分布表内,并把数据表中的各个数据列入相应的组,统计各组频数据(f )。
(6)按数据值比例画出横坐标。
(7)按频数值比例画纵坐标。以观测值数目或百分数表示。
(8)画直方图。按纵坐标画出每个长方形的高度,它代表取落在此长方形中的数据数。(注意:每个长方形的宽度都是相等的。)在直方图上应标注出公差范围(T)、样本容量(n)、样本平均值(x)、样本标准偏差值(s)和x的位置等。
考点名称:全面调查和抽样调查
- 全面调查:
就是对需要调查的对象进行逐个调查。这种方法所得资料较为全面可靠,但调查花费的人力、物力、财力较多,且调查时间较长,不适合一般企业的要求。全面调查只在产品销售范围很窄或用户很少的情况下可以采用。对品种多、产量大、销售范围广的产品,就不适用全面调查,而可以采用抽样调查。
抽样调查:
是从需要调查对象的总体中,抽取若干个个体即样本进行调查,并根据调查的情况推断总体的特征的一种调查方法。
抽样调查可以把调查对象集中在少数样本上,并获得与全面调查相近的结果。这是一种较经济的调查方法,因而被广泛采用。抽样调查是从研究对象的总体中抽取一部分个体作为样本进行调查,据此推断有关总体的数字特征。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |