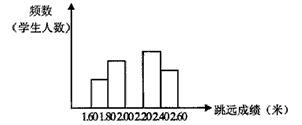
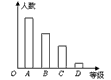
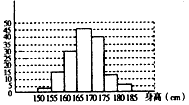
对某班学生一次数学测试成绩进行统计分析,各分数段的人数如图所示(分数取正整数),请观察图形,并回答下列问题:(1)该班有多少名学生?(2)89.5~99.5这一组的频数、频率分别-八年级数学
中位数和众数这两个统计量的特点都是能够避免极端数据,但缺点是没有完全利用数据所反映出来的信息。
由于各个统计量有各自的特征,所以需要我们根据实际问题来选择合适的统计量。
当然,出现极端数据不一定用中位数,一般,统计上有一个方法,就要认为这个数据不是来源于这个总体的,因而把这个数据去掉。比如大家熟悉的跳水比赛评分,为什么要去掉一个最高分、一个最低分呢,就认为这两个分不是来源于这个总体,不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是,我们处理的数据,大部分是对称的数据,数据符合或者近似符合正态分布。这时候,均值(平均数)、中位数和众数是一样的。
区别:
只有在数据分布偏态(不对称)的情况下,才会出现均值、中位数和众数的区别。所以说,如果是正态的话,用哪个统计量都行。如果偏态的情况特别严重的话,可以用中位数。
除了需要刻画平均水平的统计量,统计中还有刻画数据波动情况的统计量。比如,平均数同样是5,它所代表的数据可能是1、3、5、7、9,可能是4、4.5、5、5.5、6。也就是说5所代表的不同组数据的波动情况是不一样的。怎样刻画数据的波动情况呢?很自然的想法就是用最大值减最小值,即求一组数据的极差。数学中还有方差、标准差等许多用来刻画数据特征的统计量。当然这些都是教师感兴趣、值得了解的内容,不是小学数学的教学要求。
(1)公式法:
 ;
; (2)加权平均数公式:
 。
。 考点名称:频数与频率
- 频数:一般我们称落在不同小组中的数据个数为该组的频数。
频率:频数与数据总数的比值为频率。频率反映了各组频数的大小在总数中所占的分量。 频数:
在一组依大小顺序排列的测量值中,当按一定的组距将其分组时出现在各组内的测量值的数目。
如有一组测量数据,数据的总个数N=148最小的测量值xmin=0.03,最大的测量值xmax=31.67,按组距为△x=3.000将148个数据分为11组,其中分布在15.05~18.05范围内的数据有26个,则称该数据组的频数为26。频率:
如在314159265358979324中,‘9’出现的频数是3,出现的频率是3/18=16.7%
频数也称“次数”,对总数据按某种标准进行分组,统计出各个组内含个体的个数。而频率则每个小组的频数与数据总数的比值。
在变量分配数列中,频数(频率)表明对应组标志值的作用程度。
频数(频率)数值越大表明该组标志值对于总体水平所起的作用也越大,反之,频数(频率)数值越小,表明该组标志值对于总体水平所起的作用越小。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:红星中学团委为汶川地震灾区组织献爱心捐献活动,小明对本班同学的捐款情况进行了统计,其中捐10元的人数占全班总人数的.小明还绘制了频数分布直方图.(1)请求出小明所在班级-九年级数学
下一篇:在如图所示的频数分布直方图中,共测量了()名学生的身高,人数最多的身高段占全体被测者的比例是()-八年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |