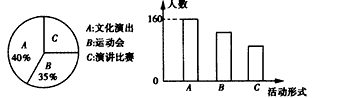
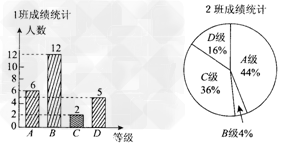
某校对中考前一次数学模拟考试进行抽样分析,把样本成绩按分数段分成A、B、C、D、E五组(每组成绩含最低分,不含最高分)进行统计,并将结果绘制成下面两幅统计图,请根据图中-九年级数学
7、作用不同
平均数:是统计中最常用的数据代表值,比较可靠和稳定,因为它与每一个数据都有关,反映出来的信息最充分。平均数既可以描述一组数据本身的整体平均情况,也可以用来作为不同组数据比较的一个标准。因此,它在生活中应用最广泛,比如我们经常所说的平均成绩、平均身高、平均体重等。
中位数:作为一组数据的代表,可靠性比较差,因为它只利用了部分数据。但当一组数据的个别数据偏大或偏小时,用中位数来描述该组数据的集中趋势就比较合适。
众数:作为一组数据的代表,可靠性也比较差,因为它也只利用了部分数据。。在一组数据中,如果个别数据有很大的变动,且某个数据出现的次数最多,此时用该数据(即众数)表示这组数据的“集中趋势”就比较适合。
中位数:
①将数据按大小顺序排列;
②当数据个数为奇数时,中间的那个数据就是中位数;
当数据个数为偶数时,居于中间的两个数据的平均数才是中位数。
众数:找出频数最多的数据,若几个数据频数最多且相同,此时众数就是这几个数据。
考点名称:条形图
- 条形图定义:
用一个单位长度表示一定的数量,根据数量的多少画成长短不同的条形,条形的宽度必须保持一致,然后把这些条形排列起来,这样的统计图叫做条形统计图。它可以表示出每个项目的具体数量。 条形图特点:
(1)能够显示每组中的具体数据;
(2)易于比较数据之间的差别。
描绘条形图的3要素:组数、组宽度、组限。
1.组数
把数据分成几组,指导性的经验是将数据分成5~10组。
2.组宽度
通常来说,每组的宽度是一致的。组数和组宽度的选择就不是独立决定的,一个经验标准是:
近似组宽度=(最大值-最小值)/组数
然后根据四舍五入确定初步的近似组宽度,之后根据数据的状况进行调整。
3.组限
分为组下限(进入该组的最小可能数据)和组上限(进入该组的最大可能数据),并且一个数据只能在一个组限内。
绘画条形图时,不同组之间是有空隙的;而绘画直方图时,不同组之间是没有空隙的。
使用条形图的情况:
轴标签过长;
显示的数值是持续型的。条形图具有下列图表子类型:
簇状条形图和三维簇状条形图 簇状条形图比较各个类别的值。在簇状条形图中,通常沿垂直轴组织类别,而沿水平轴组织数值。三维簇状条形图以三维格式显示水平矩形,而不以三维格式显示数据。堆积条形图和三维堆积条形图 堆积条形图显示单个项目与整体之间的关系。三维堆积条形图以三维格式显示水平矩形,而不以三维格式显示数据。
百分比堆积条形图和三维百分比堆积条形图 此类型的图表比较各个类别的每一数值所占总数值的百分比大小。三维百分比堆积条形图表以三维格式显示水平矩形,而不以三维格式显示数据。
水平圆柱图、圆锥图和棱锥图 水平圆柱图、圆锥图和棱锥图可以使用为矩形条形图提供的簇状图、堆积图和百分比堆积图,并且它们以完全相同的方式显示和比较数据。唯一的区别是这些图表类型显示圆柱、圆锥和棱锥形状而不是水平矩形。
- 制作条形图的步骤:
(1)根据统计资料整理数据,一般整理成表格形式;
(2)画出横轴、纵轴,确定它们所表示的项目,选定标尺,按一定比例作为长度单位,长短要适中,根据数据的大小对应标出;
(3)画直条,条形的高与数据的大小成比例。条形的宽度、间隔要一致;
(4)写上统计总标题、制图日期及数量单位。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:有200名待业人员参加某企业甲、乙、丙三个部门的招聘,到各部门报名的人数百分比见图表1,该企业各部门的录取率见图表2,(部门录取率=×100%)(1)到乙部门报名的人数有()人,乙-九年级数学
下一篇:八年级一班要组织暑假旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去上海世博会参观的学生数”的扇形圆心角为60°,则下列说法正确的是[]A、想去上海-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

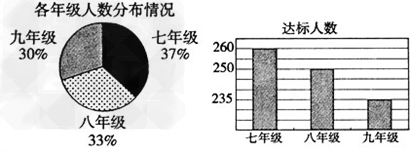
![如图所示是甲、乙两个家庭的支出费用的扇形统计图,下面对食品支出费用的判断正确的是[]A.甲户比乙户多B.乙户比甲户多C.甲、乙两户一样多D.无法确定哪一户多-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/127/2019-12-18/e950950c560c17ae3213ba778654b84b.png)