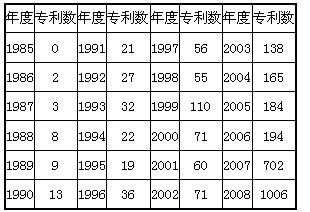
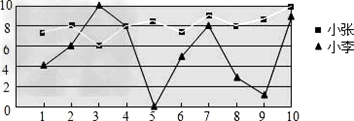
小明调查了2002年12月15日这一天的气温变化情况,通常是每天调查四次,分别是2时、8时、14时、20时,结果如下表:(1)请据此作出合适的统计图;(2)请求出这一天的平均气温?(3)-七年级数学
题文
| 小明调查了2002年12月15日这一天的气温变化情况,通常是每天调查四次,分别是2时、8时、14时、20时,结果如下表: (1)请据此作出合适的统计图; (2)请求出这一天的平均气温? (3)从这些数据中你能得哪些信息,有如何感受? |
 |
答案
| 解:(1)如下图. (2)(4+7+15+12)÷4=9.5℃, (3)14时的气温最高,2时的气温最低,这天的温差15﹣4=11℃.
|
据专家权威分析,试题“小明调查了2002年12月15日这一天的气温变化情况,通常是每天调查..”主要考查你对 折线图,平均数 等考点的理解。关于这些考点的“档案”如下:
折线图平均数
考点名称:折线图
- 定义:
用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段把各点顺次连接起来。
折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况。 - 折线图特点:
易于显示数据的变化的规律和趋势。可以用来作股市的跌涨和统计气温。
折线图具有下列图表子类型:
折线图和带数据标记的折线图 折线图用于显示随时间或有序类别而变化的趋势,可能显示数据点以表示单个数据值,也可能不显示这些数据点。
在有很多数据点并且它们的显示顺序很重要时,折线图尤其有用。如果有很多类别或者数值是近似的,则应该使用不带数据标记的折线图。 - 几种折线图区别:
堆积折线图和带数据标记的堆积折线图:
堆积折线图用于显示每一数值所占大小随时间或有序类别而变化的趋势,可能显示数据点以表示单个数据值,也可能不显示这些数据点。如果有很多类别或者数值是近似的,则应该使用无数据点堆积折线图。
提示:为更好地显示此类型的数据,您可能要考虑改用堆积面积图。
百分比堆积折线图和带数据标记的百分比堆积折线图:
百分比堆积折线图用于显示每一数值所占百分比随时间或有序类别而变化的趋势。
三维折线图:三维折线图将每一行或列的数据显示为三维标记。
三维折线图具有可修改的水平轴、垂直轴和深度轴。 - 制作折线图的步骤:
(1)根据统计资料整理数据;
(2)作平面直角坐标系,横轴、纵轴都标上单位长度,取长适当;一般横轴表示时间(或先后次数),纵轴表示时间序列数据;
(3)根据数据描点。并按先后顺序将点用折线连接起来。 - 折线图制作技巧:
1.“字体”的处理
建议:取消图表的字体“自动缩放”功能,这样可防止在变动图表大小时,图表项的字体发生不必要的改变。
取消所有图表项的“自动缩放”功能,要取消所有图表项的字体“自动缩放”功能,取消图表区的“字体缩放“功能即可。可通过双击图表区,并调出“图表区格式”对话框,切换到“字体”选项卡,取消“自动缩放”前面的复选框的选择,这样便是取消了所有图表项的字体缩放功能,然后分别对各图表项的字体按需要设定字体大小。
2.“网格线”的处理
使用“折线图”或“散点图”时,尤其要注意淡化网格线对数据系列的影响,可取消网格线或是将其设为虚线,并改为浅色。
3. 数据系列格式的设置
一般不使用默认的格式设置,根据自己的需求改变“线形“或是“数据标记”及“填充”。
考点名称:平均数
- 平均数:
是指在一组数据中所有数据之和再除以数据的个数。平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。
解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。
在统计工作中,平均数(均值)和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。 - 平均数的分类:
(1)算术平均数:一般地,如果有n个数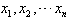 ,那么
,那么  ,叫做这n个数的算术平均数。
,叫做这n个数的算术平均数。
(2)加权平均数:一组数据 点的权分别为
点的权分别为 ,那么称
,那么称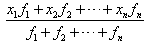 为这n个数的加权平均数。
为这n个数的加权平均数。
(3)样本平均数:样本中所有个体的平均数。
(4)总体平均数:总体中所有个体的平均数,统计学中常用样本的平均数估计总体的平均数。 平均数、中位数和众数关系:
联系:
平均数、中位数和众数都是来刻画数据平均水平的统计量,它们各有特点。对于平均数大家比较熟悉,中位数刻画了一组数据的中等水平,众数刻画了一组数据中出现次数最多的情况。
平均数非常明显的优点之一是,它能够利用所有数据的特征,而且比较好算。另外,在数学上,平均数是使误差平方和达到最小的统计量,也就是说利用平均数代表数据,可以使二次损失最小。因此,平均数在数学中是一个常用的统计量。但是平均数也有不足之处,正是因为它利用了所有数据的信息,平均数容易受极端数据的影响。
例如,在一个单位里,如果经理和副经理工资特别高,就会使得这个单位所有成员工资的平均水平也表现得很高,但事实上,除去经理和副经理之外,剩余所有人的平均工资并不是很高。这时,中位数和众数可能是刻画这个单位所有人员工资平均水平更合理的统计量。
中位数和众数这两个统计量的特点都是能够避免极端数据,但缺点是没有完全利用数据所反映出来的信息。
由于各个统计量有各自的特征,所以需要我们根据实际问题来选择合适的统计量。
当然,出现极端数据不一定用中位数,一般,统计上有一个方法,就要认为这个数据不是来源于这个总体的,因而把这个数据去掉。比如大家熟悉的跳水比赛评分,为什么要去掉一个最高分、一个最低分呢,就认为这两个分不是来源于这个总体,不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是,我们处理的数据,大部分是对称的数据,数据符合或者近似符合正态分布。这时候,均值(平均数)、中位数和众数是一样的。区别:
只有在数据分布偏态(不对称)的情况下,才会出现均值、中位数和众数的区别。所以说,如果是正态的话,用哪个统计量都行。如果偏态的情况特别严重的话,可以用中位数。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |



![一天中的气温变化各不相同,为了直观表示出一天的气温变化情况,气象员通常把它制成[]A.扇形统计图B.折线统计图C.条形统计图D.复式统计图-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/128/2019-12-18/573efd418baa070cecf582bea324da20.png)