水是眼波横,山是眉峰聚。欲问行人去那边?眉眼盈盈处。才始送春归,又送君归去。若到江南赶上春,千万和春住。
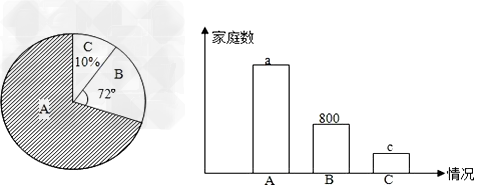
为了节约资源,保护环境,某中学课外实践小组的同学,利用业余时间对本城区居民家庭使用超薄塑料袋的情况进行了抽样调查.统计情况如图所示,其中A为“不再使用”,B为“明显减少-九年级数学
题文
| 为了节约资源,保护环境,某中学课外实践小组的同学,利用业余时间对本城区居民家庭使用超薄塑料袋的情况进行了抽样调查.统计情况如图所示,其中A为“不再使用”,B为“明显减少了使用量”,C为“没有明显变化” (1)本次抽样的样本容量是 _________ ; (2)图中a= _________ (户),c= _________ (户); (3)若被调查的家庭占全城区家庭数的10%,则该城区不再使用超薄塑料袋的家庭数约为 _________ . |
 |
答案
| 解:(1)样本容量=B的数量除以B所占样本的比例, 故可得样本容量为:800×  ×100%=4000; ×100%=4000;(2)由题意得,c=4000×10%=400;a=4000(1﹣10%﹣20%)=2800. (3)全城家庭数为:4000÷10%=40000, 所以该城区不再使用超薄塑料袋的家庭数约为40000×70%=28000(户); 故答案为:4000、2800、400、28000. |
据专家权威分析,试题“为了节约资源,保护环境,某中学课外实践小组的同学,利用业余时..”主要考查你对 总体、个体、样本、样本容量,扇形图,用样本估算总体 等考点的理解。关于这些考点的“档案”如下:
总体、个体、样本、样本容量扇形图用样本估算总体
考点名称:总体、个体、样本、样本容量
- 掌握总体、个体、样本,样本容量的概念,能正确区分总体、个体、样本、样本容量
总体、个体、样本、样本容量,这四个概念之间其实有其内在联系,
总体:我们把所要考察的对象的全体叫做总体;
个体:把组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包含的个体的数量叫做这个样本的容量。
我们在区分这四个概念时,首先找出考察的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量。
考点名称:扇形图
- 定义:
用圆的面积代表事物总体,以扇形的面积和圆的面积的比值表示个项目占总体的百分数的统计图,叫做扇形统计图。 - 特点:
(1)用扇形的面积表示部分在总体中所占的百分比;
(2)易于显示每组数据相对于总数的大小。
作用:
能清楚地了解各部分数与总数之间的关系与比例。
扇形面积与其对应的圆心角的关系是:
扇形面积越大,圆心角的度数越大。
扇形面积越小,圆心角的度数越小。
扇形所对圆心角的度数与百分比的关系是:
圆心角的度数=百分比×360度
扇形统计图还可以画成圆柱形的。 - 制作扇形统计图的步骤:
(1)根据统计资料,整理数据,并计算出部分占整体的百分数;
(2)根据各部分占总体的百分数,计算出各部分扇形圆心角的度数;
(3)取适当半径作圆,按圆心角将圆分成几个扇形;
(4)对应标上各部分名称及占总体的百分数。
考点名称:用样本估算总体
- 用样本估计总体的两个手段:
(1)用样本的频率分布估计总体的分布;
(2)用样本的数字特征估计总体的数字特征,需要从总体中抽取一个质量较高的样本,才能不会产生较大的估计偏差,且样本的容量越大,估计的结果也就越精确。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:为了节约资源,保护环境,某中学课外实践小组的同学,利用业余时间对本城区居民家庭使用超薄塑料袋的情况进行了抽样调查.统计情况如图所示,其中A为“不再使用”,B为“明显减少-九年级数学
下一篇:某市有5500名学生参加考试,为了了解考试情况,从中抽取1000名学生的成绩进行统计分析,在这个问题中,有下述4种说法:(1)1000名考生是总体的一个样本(2)1000名学生的平均成绩-八年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |