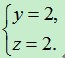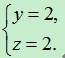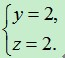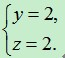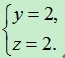方程组6x-y-z=20x2+y2+z2=1979的所有正整数解是______.-数学
题文
方程组
|
答案
∵
∵(y-z)2≥0?2yz≤y2+z2?2yz+y2+z2=2(y2+z2)?(y+z)2≤2(y2+z2) ∴(y+z)2=(6x-20)2≤2(y2+z2)=2(1979-x2) 于是(6x-20)2≤2(1979-x2)≤2×1978<632 注解到不等式(y+z)2≤2(y2+z2)有(y+z)2=(6x-20)2≤2(y2+z2)=2(1979-x2), 于是(6x-20)2≤2(1979-x2)≤2×1978<632,即-63<6x-20<63 又∵y+z=6x-20是正整数 ∴0<6x-20<63,即
再由y+z为偶数,从而y2+z2为偶数,x2为奇数,进而x为奇数. ∴x=5,7,9,11,13 ①当x=5时,
②当x=7时,
③当x=9时,
④当x=11时,解得
⑤当x=13时,解得
故答案为
|