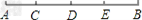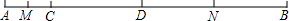已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB。(1)若A、B的位置如图1所示,试化简:|a|-|b|+|a+b|+|a-b|;(2)如图2,若|a|+|b|=8.9,MN=3,求图中-七年级数学
题文
|
已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB。 |
|
|
| (1)若A、B的位置如图1所示,试化简:|a|-|b|+|a+b|+|a-b|; (2)如图2,若|a|+|b|=8.9,MN=3,求图中以A、N、O、M、B这5个点为端点的所有线段长度的和; (3)如图3,M为AB中点,N为OA中点,且MN=2AB-15,a=-3,若点P为数轴上一点,且PA=  AB,试求点P所对应的数为多少? AB,试求点P所对应的数为多少? |
答案
| 解:(1)由已知有:a<0,b>0 ∵OA<OB ∴∣a∣<∣b∣ ∴a+b>0,a-b<0 ∴∣a∣-∣b∣+∣a+b∣+∣a-b∣=-a-b+a+b+b-a=b-a; (2)∵∣a∣+∣b∣=8.9 ∴AB=8.9 又MN=3 ∴AN+AO+AM+AB+NO+NM+NB+OM+OB+MB =(AN+NB)+(AO+OB)+(AM+MB)+AB+(NO+OM)+NM =AB+AB+AB+AB+NM+NM =4AB+2NM =4×8.9+2×3 =41.6 答:所有线段长度的和为41.6;  (3)∵a=-3, ∴OA=3, ∵M为AB的中点,N为OA的中点, ∴AM=  AB,AN= AB,AN= OA, OA,∴MN=AM-AN=  AB- AB- OA= OA= AB- AB- , ,又MN=2AB-15, ∴2AB-15=  AB- AB- , ,解得:AB=9, ∴PA=  AB=6, AB=6,若点P在点A的左边时,点P在原点的左边(图略)OP=9,故点P所对应的数为-9; 若点P在点A的右边时,点P在原点的右边(图略)OP=3,故点P所对应的数为3; 答:P所对应的数为-9或3。 |
据专家权威分析,试题“已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA..”主要考查你对 直线,线段,射线,数轴,绝对值 等考点的理解。关于这些考点的“档案”如下:
直线,线段,射线数轴绝对值
考点名称:直线,线段,射线
- 基本概念:
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意:
①线和射线无长度,线段有长度。
②直线无端点,射线有一个端点,线段有两个端点。 直线、射线、线段的基本性质:
图形 表示法 端点 延长线 能否度量 基本性质 直线 没有端点的一条线 一条线,
不要端点无 可以向两边无限延长 否 两端都没有端点,可以无限延长,不可测量的线 射线 只有一个端点的一条线 一条线,
只有一边有端点一个 可以向一边无限延长 否 一端有端点,可以向一边无限延长,不可测量的线 线段 两边都有端点的一条线 一条线,两边都有端点 两个 不能延长 能 两端都有端点,不能延长,可测量的线 - 直线、射线、线段区别:
直线没有端点,2边可无限延长;
射线有1端有端点,另一端可无限延长;
线段,有2个端点,而2个端点间的距离就是这条线段的长度。
直线除了“直”这个特点外,还有一个很重要的特点,那就是它可以向两个方向无限延伸,永远没有尽头,所以,直线是不可能度量的。因此,在画直线时,要画出没有端点的直线,表示可以无限延伸;
射线只有一个端点,可以向一个方向无限延伸,也永远没有尽头。所以,射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线,因此,射线是直线的一部分。虽然射线是直线的一部分,但由于它们都是不能度量的,所以,它们之间没有长短可以比较;
线段有两个端点,它有一定的长度,可以度量。线段也是直线的一部分。 - 各种图形表示方法:
直线:一个小写字母或两个大写字母,但前面必须加“直线”两字,如:直线l,直线m;直线AB,直线CD。
例: 直线l;直线AB。
直线l;直线AB。
射线:一个小写字母或端点的大写字母。和射线上的一个大写字母,前面必须加“射线”两字。如:射线a;射线OA。
例: 射线AB。
射线AB。
线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a。
例: 线段AB;线段a 。
线段AB;线段a 。
考点名称:数轴
- 数轴定义:
规定了唯一的原点,正方向和单位长度的一条直线叫做数轴。
数轴具有三要素:
原点、正方向和单位长度,三者缺一不可。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:已知线段AB=5cm,在直线AB上画线段BC=2cm,则AC的长是[]A、3cmB、7cmC、3cm或7cmD、无法确定-七年级数学
下一篇:已知,如图:已知线段AB,点C在AB的延长线上,AC=BC,D在AB的反向延长线上,BD=DC。⑴在图上画出点C和点D的位置;⑵设线段AB长为x,则BC=____;AD=____;(用含x的代数式表示)⑶若-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |