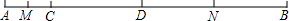题文

如图所示的方格纸中，点C是∠AOB的边OB上的一点，按下列要求画图并回答问题． （1）过点C画OB的垂线，交OA于点D，该垂线是否经过格点？若经过格点，请在图中标出垂线所经过的格点； （2）过点C画OA的垂线，垂足为E． ①线段CE的长度是点C到______的距离，______是点D到OB的距离； ②因为直线外一点与直线上各点连接的所有线段中，垂线段最短，所以线段CD、CE、OD、OC这四条线段大小关系是______（用“＜”号连接）； （3）过D点画直线DF∥OB，若∠AOB=x°，则∠ADC=______（用含x的代数式表示）．

题型：解答题  难度：中档

答案

（1）如图所示，图中该垂线经过的格点有点D、M、N， （2）如图所示，①∵CE⊥OA，CD⊥OB， ∴线段CE的长度是点C到OA的距离，CD是点D到OB的距离； ②如图，∵CD⊥OC，CD＜OC， ∴CD＜OC＜OD， ∵CE⊥OA， ∴CE＜CD， ∴CE＜CD＜OC＜OD， （3）如图所示，∵CD⊥OB，∠AOB=x°， ∴∠ADC=90°+x°， 故答案为OA，DC；CE＜CD＜OC＜OD；90°+x°．

据专家权威分析，试题“如图所示的方格纸中，点C是∠AOB的边OB上的一点，按下列要求画图并..”主要考查你对  直线，线段，射线，垂直平分线的性质  等考点的理解。关于这些考点的“档案”如下：

直线，线段，射线垂直平分线的性质

考点名称：直线，线段，射线

• 基本概念：
  直线：一根拉得很紧的线，就给我们以直线的形象，直线是直的，并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
  线段：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
  射线：直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
  注意：
  ①线和射线无长度，线段有长度。
  ②直线无端点，射线有一个端点，线段有两个端点。
  

• 直线、射线、线段的基本性质：

  	图形	表示法	端点	延长线	能否度量	基本性质
  直线	没有端点的一条线	一条线, 不要端点	无	可以向两边无限延长	否	两端都没有端点,可以无限延长,不可测量的线
  射线	只有一个端点的一条线	一条线, 只有一边有端点	一个	可以向一边无限延长	否	一端有端点,可以向一边无限延长,不可测量的线
  线段	两边都有端点的一条线	一条线,两边都有端点	两个	不能延长	能	两端都有端点,不能延长,可测量的线

• 直线、射线、线段区别：
  直线没有端点,2边可无限延长；
  射线有1端有端点，另一端可无限延长；
  线段,有2个端点,而2个端点间的距离就是这条线段的长度。
  
  直线除了“直”这个特点外，还有一个很重要的特点，那就是它可以向两个方向无限延伸，永远没有尽头，所以，直线是不可能度量的。因此，在画直线时，要画出没有端点的直线，表示可以无限延伸；
  射线只有一个端点，可以向一个方向无限延伸，也永远没有尽头。所以，射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线，因此，射线是直线的一部分。虽然射线是直线的一部分，但由于它们都是不能度量的，所以，它们之间没有长短可以比较；
  线段有两个端点，它有一定的长度，可以度量。线段也是直线的一部分。

• 各种图形表示方法：
  直线：一个小写字母或两个大写字母，但前面必须加“直线”两字，如：直线l，直线m；直线AB，直线CD。
  例：直线l；直线AB。
  射线：一个小写字母或端点的大写字母。和射线上的一个大写字母，前面必须加“射线”两字。如：射线a；射线OA。
  例：射线AB。
  线段：用表示端点的大写字母表示，如线段AB；用一个小写字母表示，如线段a。
  例：线段AB；线段a 。

考点名称：垂直平分线的性质

• 垂直平分线的概念：
  垂直于一条线段并且平分这条线段的直线，叫做这条线段的垂直平分线（中垂线）。
  如图：直线MN即为线段AB的垂直平分线。
  

• 垂直平分线的性质：
  1.垂直平分线垂直且平分其所在线段。
  2.垂直平分线上任意一点，到线段两端点的距离相等。
  逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
  3.如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。
  4.三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相 等。
  （此时以外心为圆心，外心到顶点的长度为半径，所作的圆为此三角形的外接圆。）
  
  判定：
  ①利用定义；
  ②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
  （即线段垂直平分线可以看成到线段两端点距离相等的点的集合）

• 尺规作法：（用圆规作图）
  1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。
  2、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线。得到两个交点(两交点交与线段的异侧)。
  3、连接这两个交点。
  原理：等腰三角形的高垂直平分底边。