下列说法正确的个数是()(1)菱形ABCD的对角线AC、BD相交于点O,O到菱形四条边的距离都相等;(2)两条对角线互相垂直且相等的四边形是正方形;(3)所有的定理都有逆定理;(4)矩形-数学
题文
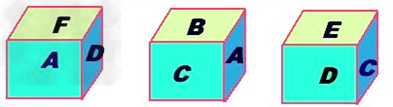
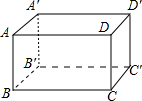
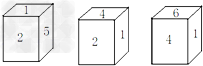
| 下列说法正确的个数是( ) (1)菱形ABCD的对角线AC、BD相交于点O,O到菱形四条边的距离都相等;(2)两条对角线互相垂直且相等的四边形是正方形;(3)所有的定理都有逆定理;(4)矩形的两条对角线相交于点O,∠AOD=120°,AB=4cm,则矩形的面积为16
|
答案
| (1)菱形的对角线垂直,并且每一条对角线平分一组对角,所以点O是四个角平分线的交点,根据角平分线上的点到角的两边的距离相等,可知点O到菱形四条边的距离都相等.故说法正确; (2)两条对角线互相垂直且相等的平行四边形才是正方形,故说法错误; (3)任何一个命题都有逆命题,但并不是所有的定理都有逆定理,故说法错误; (4)∠AOD=120°,所以∠ADO=30°,又因为∠A=90°所以BD=8cm,由勾股定理得AD=4
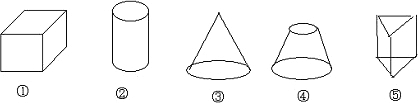
(5)球的主视图、左视图、俯视图都是圆.故说法正确. 所以说法正确的有(1)(4)(5),共3个. 故选C. |
据专家权威分析,试题“下列说法正确的个数是()(1)菱形ABCD的对角线AC、BD相交于点O,O到..”主要考查你对 认识立体几何图形,矩形,矩形的性质,矩形的判定,菱形,菱形的性质,菱形的判定,正方形,正方形的性质,正方形的判定,视图(盲区) 等考点的理解。关于这些考点的“档案”如下:
认识立体几何图形矩形,矩形的性质,矩形的判定菱形,菱形的性质,菱形的判定正方形,正方形的性质,正方形的判定视图(盲区)
考点名称:认识立体几何图形
- 立体几何图形:
从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一。有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形。由一个或多个面围成的可以存在于现实生活中的三维图形。点动成线,线动成面,面动成体。即由面围成体,看一个体最多看到立体图形实物三个面。 - 常见立体几何图形及性质:
①正方体:
有8个顶点,6个面。每个面面积相等(或每个面都有正方形组成)。有12条棱,每条棱长的长度都相等。(正方体是特殊的长方体)
②长方体:
有8个顶点,6个面。每个面都由长方形或相对的一组正方形组成。有12条棱,相对的4条棱的棱长相等。
③圆柱:
上下两个面为大小相同的圆形。有一个曲面叫侧面。展开后为长方形或正方形或平行四边形。有无数条高,这些高的长度都相等。
④圆锥:
有1个顶点,1个曲面,一个底面。展开后为扇形。只有1条高。四面体有1个顶点,四面六条棱高。
⑤直三棱柱:
三条侧棱切平行,上表面和下表面是平行且全等的三角形。
⑥球:
球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体。 - 常见的立体几何图形视图:
几何图形 图形 长方体 
正方体 
圆锥 
圆柱 
圆锥 
球 
考点名称:矩形,矩形的性质,矩形的判定
- 矩形:
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。 矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形- 矩形的判定:
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。 - 黄金矩形:
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。如希腊的巴特农神庙等。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |