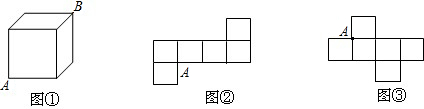
如图1所示为一个无盖的正方体纸盒,现将其展开成平面图,如图2所示。已知展开图中每个正方形的边长为1。(1)求该展开图中可画出最长线段的长度,并求出这样的线段可画几条。(-八年级数学
题文
| 如图1所示为一个无盖的正方体纸盒,现将其展开成平面图,如图2所示。已知展开图中每个正方形的边长为1。 |
 |
| (1)求该展开图中可画出最长线段的长度,并求出这样的线段可画几条。 (2)试比较立体图中∠ABC与平面展开图中的∠A′B′C′大小关系。 |
答案
解:(1)在平面展开图中可画出最长的线段长为 , ,如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,  答:这样的线段可画4条(另三条用虚线标出).  (2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,∴∠BAC=45°. 在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=  ,B'C'= ,B'C'=  . .又∵A′B′2+B′C′2=A′C′2,由勾股定理的逆定理可得△A'B'C'为直角三角形. 又∵A′B′=B′C′,∴△A′B′C′为等腰直角三角形. ∴∠B′A′C′=45°. ∴∠BAC与∠B′A′C′相等. |
据专家权威分析,试题“如图1所示为一个无盖的正方体纸盒,现将其展开成平面图,如图2所..”主要考查你对 几何体的展开图 等考点的理解。关于这些考点的“档案”如下:
几何体的展开图
考点名称:几何体的展开图
- 有些立体图形是由一些平面图形围成的,将它们的表面适当的剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图。
几何体展开图规律:
1.沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;
2.同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图。
注意:
①正方体展开头记忆口诀:
正方体盒巧展开,六个面儿七刀裁;
十四条边布周围,十一类图记分明;
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
②在正方体的展开图中,一条直线上的小正方形不会超过四个。
③正方体的展开图不会有"田"字形,"凹"字形的形状。- 图形展开图:
1.圆柱展开图: →→
→→
2.圆锥展开图: →→
→→
3.长方体展开图: →→
→→
4.正方体展开图: →→
→→
5.三棱柱展开图: →→
→→
6.三棱锥展开图: →→
→→
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![下列各组均由六个大小一样的正方形组成,其中可作为正方体的展开图的是[]A.B.C.D.-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/144/2020-01-02/6b1d1e7c821b024d0093c456e297352a.png)

![如图是一个正方体的展开图,每个图内都标注了字母,则展开图中,与面E相对的是[]A.面AB.面BC.面CD.面D-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/144/2020-01-02/b99bc027b07f62623a84296524d78cd7.png)
![一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该正方体中和“毒”字相对的字是[]A.卫B.防C.讲D.生-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/144/2020-01-02/8779cae56d59fa390c6f7ed359cc3a49.gif)
