(答案不全)(1)在如图(1)所示的正方体表面展开图中的三个空白正方形内各填入一个质数,使该图复原成正方体后,三组对面上的两数之和都相等.(2)图(2)是由四个如图(1)所示的正方-数学
题文
| (答案不全) (1)在如图(1)所示的正方体表面展开图中的三个空白正方形内各填入一个质数,使该图复原成正方体后,三组对面上的两数之和都相等. (2)图(2)是由四个如图(1)所示的正方体拼成的长方体,其中有阴影的面上为合数,无阴影的面上为质数,并且整个表面上任意两个相邻正方形内的数都不是图(1)所示的正方体相对面上的两数.已知长方体正面上的四个数之和为质数,那么其左侧面上的数是______(填具体数). (3)如果把图(2)中的长方体从中间等分成左右两个小长方体,它们各自表面上的各数之和分别为S左和S右,那么S左与S右的大小关系是S左______S右. 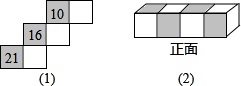 |


 →→
→→
 →→
→→
 →→
→→
 →→
→→
 →→
→→
 →→
→→
![下列各组均由六个大小一样的正方形组成,其中可作为正方体的展开图的是[]A.B.C.D.-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/144/2020-01-02/6b1d1e7c821b024d0093c456e297352a.png)

![如图是一个正方体的展开图,每个图内都标注了字母,则展开图中,与面E相对的是[]A.面AB.面BC.面CD.面D-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/144/2020-01-02/b99bc027b07f62623a84296524d78cd7.png)
![一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该正方体中和“毒”字相对的字是[]A.卫B.防C.讲D.生-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/144/2020-01-02/8779cae56d59fa390c6f7ed359cc3a49.gif)
