下列说法:①若∠1与∠2是同位角,则∠1=∠2②等腰三角形的高,中线,角平分线互相重合③对角线互相垂直且相等的四边形是正方形④等腰梯形是轴对称图形,但不是中心对称图形⑤平分弦的-数学
正方形的性质:
1、边:两组对边分别平行;四条边都相等;相邻边互相垂直
2、内角:四个角都是90°;
3、对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;
4、对称性:既是中心对称图形,又是轴对称图形(有四条对称轴);
5、正方形具有平行四边形、菱形、矩形的一切性质;
6、特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;
正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
7、在正方形里面画一个最大的圆,该圆的面积约是正方形面积的78.5%;
正方形外接圆面积大约是正方形面积的157%。
8、正方形是特殊的长方形。
正方形的判定:
判定一个四边形为正方形的一般顺序如下:先证明它是平行四边形,再证明它是菱形(或矩形),最后证明它是矩形(或菱形)。
1:对角线相等的菱形是正方形。
2:有一个角为直角的菱形是正方形。
3:对角线互相垂直的矩形是正方形。
4:一组邻边相等的矩形是正方形。
5:一组邻边相等且有一个角是直角的平行四边形是正方形。
6:对角线互相垂直且相等的平行四边形是正方形。
7:对角线相等且互相垂直平分的四边形是正方形。
8:一组邻边相等,有三个角是直角的四边形是正方形。
9:既是菱形又是矩形的四边形是正方形。
有关计算公式:
若S为正方形的面积,C为正方形的周长,a为正方形的边长,则
正方形面积计算公式:S =a×a(即a的2次方或a的平方),或S=对角线×对角线÷2;
正方形周长计算公式: C=4a 。
S正方形= 。(正方形边长为a,对角线长为b)
。(正方形边长为a,对角线长为b)
考点名称:垂直于直径的弦
垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
注:
(1)定理中的直径过圆心即可,可以是直径、半径、过圆心的直线或线段;
(2)此定理是证明等线段、等角、垂直的主要依据,同时也为圆的有关计算提供了方法和依据。
垂径定理的推论:
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧
推论二:弦的垂直平分线经过圆心,并且平分这条弦所对的弧
推论三:平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧
推论四:在同圆或者等圆中,两条平行弦所夹的弧相等
(证明时的理论依据就是上面的五条定理)
但是在做不需要写证明过程的题目中,可以用下面的方法进行判断:一条直线,在下列5条中只要具备其中任意两条作为条件,就可以推出其他三条结论
1.平分弦所对的优弧
2.平分弦所对的劣弧
(前两条合起来就是:平分弦所对的两条弧)
3.平分弦 (不是直径)
4.垂直于弦
5.经过圆心
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

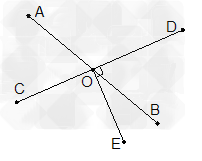
![如图,在□ABCD中,AB=4cm,AD=7cm,∠ABC平分线交AD于E,交CD的延长线于点F,则DF=[]A.2cmB.3cmC.4cmD.5cm-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/149/2020-01-04/cf55cc02803f9566cd49969bf0ed90f4.gif)
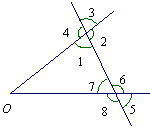
![图中,与∠1成同位角的个数是[]A.2个B.3个C.4个D.5个-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/149/2020-01-04/9c91841e0e79a92fc284bdf8ba2294a2.png)

