如图所示,直线AB、CD被直线EF所截,(1)量得∠1=80°,∠2=80°,则AB∥CD,根据是______;(2)量得∠3=100°,∠4=100°,则AB∥CD,根据是______;(3)量得∠2=80°,∠4=100°,则AB∥CD,-数学
题文
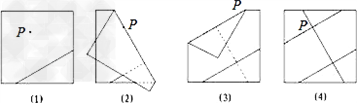
| 如图所示,直线AB、CD被直线EF所截, (1)量得∠1=80°,∠2=80°,则AB∥CD,根据是______; (2)量得∠3=100°,∠4=100°,则AB∥CD,根据是______; (3)量得∠2=80°,∠4=100°,则AB∥CD,根据是______.  |

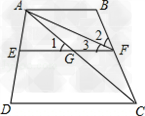

![如图,下列说法中,正确的是[]A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/150/2020-01-07/6a9802b7a026a5297753da5eca5ae992.png)