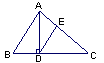
如图,AB是⊙O的的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD//OC,弦DF⊥AB于点G。(1)求证:点E是的中点;(2)求证:CD是⊙O的切线。-九年级数学
圆心角:
顶点在圆心的角叫做圆心角。
圆周角:
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上,它的两边为圆的两条弦。
圆心角特征识别:
①顶点是圆心;
②两条边都与圆周相交。
计算公式:
①L(弧长)=n/180Xπr(n为圆心角度数,以下同);
②S(扇形面积) = n/360Xπr2;
③扇形圆心角n=(180L)/(πr)(度)。
④K=2Rsin(n/2) K=弦长;n=弦所对的圆心角,以度计。
圆心角定理:
圆心角的度数等于它所对的弧的度数。
理解:(定义)
(1)等弧对等圆心角
(2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.
(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.
(4)圆心角的度数和它们对的弧的度数相等.
推论:
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等
与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明:分三种情况讨论,始终做直径COD,利用等腰三角形等腰底角相等,外角等于两内角之和来证明。
圆周角定理推论:
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中,同弧或等弧所对的圆周角相等,相等圆周角所对的弧也相等。(不在同圆或等圆中其实也相等的。注:仅限这一条。)
④半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中,圆周角相等<=>弧相等<=>弦相等。
考点名称:直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)
直线与圆的位置关系:
直线与圆的位置关系有三种:直线与圆相交,直线与圆相切,直线与圆相离。
(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点AB与⊙O相交,d<r;
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,这个唯一的公共点叫做切点。AB与⊙O相切,d=r。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离,AB与圆O相离,d>r。(d为圆心到直线的距离)- 直线与圆的三种位置关系的判定与性质:
(1)数量法:通过比较圆心O到直线距离d与圆半径的大小关系来判定,
如果⊙O的半径为r,圆心O到直线l的距离为d,则有:
直线l与⊙O相交 d<r;
d<r;
直线l与⊙O相切 d=r;
d=r;
直线l与⊙O相离 d>r;
d>r;
(2)公共点法:通过确定直线与圆的公共点个数来判定。
直线l与⊙O相交 d<r
d<r 2个公共点;
2个公共点;
直线l与⊙O相切 d=r
d=r 有唯一公共点;
有唯一公共点;
直线l与⊙O相离 d>r
d>r 无公共点 。
无公共点 。
圆的切线的判定和性质
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
(2)切线的性质定理:圆的切线垂直于经过切点的半径。
切线长:
在经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长。
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 - 直线与圆的位置关系判定方法:
平面内,直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0的位置关系判断一般方法是:
1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x2+y2+Dx+Ey+F=0,即成为一个关于x的方程
如果b2-4ac>0,则圆与直线有2交点,即圆与直线相交。
如果b2-4ac=0,则圆与直线有1交点,即圆与直线相切。
如果b2-4ac<0,则圆与直线有0交点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x轴),将x2+y2+Dx+Ey+F=0化为(x-a)2+(y-b)2=r2。
令y=b,求出此时的两个x值x1、x2,并且规定x1<x2,那么:
当x=-C/A<x1或x=-C/A>x2时,直线与圆相离;
当x1<x=-C/A<x2时,直线与圆相交。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |