题文

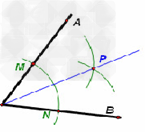
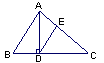
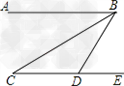
如图a，∠EBF=90°，请按下列要求准确画图： 1：在射线BE、BF上分别取点A、C，使BC＜AB＜2BC，连接AC得直角△ABC； 2：在AB边上取一点M，使AM=BC，在射线CB边上取一点N，使CN=BM，直线AN、CM相交于点P． （1）请用量角器度量∠APM的度数为______；（精确到1°） （2）请用说理的方法求出∠APM的度数； （3）若将①中的条件“BC＜AB＜2BC”改为“AB＞2BC”，其他条件不变，你 能自己在图b中画出图形，求出∠APM的度数吗？

题型：解答题  难度：中档

答案

（1）45°． （2）过点A作AK⊥AB，且AK=CN，连接CK、MK， ∴四边形ANCK是平行四边形． ∵CN=MB，∴AK=MB， ∵AM=CB，∠B=∠KAM， ∴△AKM≌△BMC． ∴∠AKM=∠BMC，KM=MC． ∵∠AKM+∠AMK=90°， ∴∠BMC+∠AMK=90°． ∴∠KMC=90°． ∴△KMC是等腰直角三角形． ∴∠MCK=45°． ∵CK∥AN， ∴∠APM=∠MCK=45°． （3）过点A作AK⊥AB，且AK=CN，连接CK、MK． ∴四边形ANCK是平行四边形． ∵CN=MB，∴AK=MB， ∵AM=CB，∠B=∠KAM， ∴△AKM≌△BMC． ∴∠AKM=∠BMC，KM=MC． ∵∠AKM+∠AMK=90°， ∴∠BMC+∠AMK=90°． ∴∠KMC=90°． ∴△KMC是等腰直角三角形． ∴∠MCK=45°． ∵CK∥AN， ∴∠APM+∠MCK=180°． ∴∠APM=135°．

据专家权威分析，试题“如图a，∠EBF=90°，请按下列要求准确画图：1：在射线BE、BF上分别取..”主要考查你对  平行线的性质，平行线的公理，三角形全等的判定，勾股定理的逆定理  等考点的理解。关于这些考点的“档案”如下：

平行线的性质，平行线的公理三角形全等的判定勾股定理的逆定理

考点名称：平行线的性质，平行线的公理

• 平行公理：过直线外一点有且只有一条直线与已知直线平行。
  推论（平行线的传递性）：平行同一直线的两直线平行。
  ∵a∥c，c ∥b
  ∴a∥b。

  平行线的性质：
  1. 两条平行被第三条直线所截，同位角相等。
  简单说成：两直线平行，同位角相等。
  2. 两条平行线被第三条直线所截，内错角相等。
  简单说成：两直线平行，内错角相等。
  3 . 两条平行线被第三条直线所截，同旁内角互补。
  简单说成：两直线平行，同旁内角互补。

• 平行线的性质公理注意：
  ①注意条件“经过直线外一点”，若经过直线上一点作已知直线的平行线，就与已知直线重合了；
  ②平行公理体现了平行线的存在性和唯一性；
  ③平行公理的推论体现了平行线的传递性。
  ④在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论。这是平行线特有的性质。不要一提同位角或内错角就认为他们相等，一提同旁内角就认为互补，若没有两直线平行的条件，他们是不成立的。
  

考点名称：三角形全等的判定

• 三角形全等判定定理：
  1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”)，这一条也说明了
  三角形具有稳定性的原因。
  2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
  3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
  4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)
  5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边，直角边”) 所以：SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
  注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。

• 三角形全等的判定公理及推论：
  (1)“边角边”简称“SAS”
  (2)“角边角”简称“ASA”
  (3)“边边边”简称“SSS”
  (4)“角角边”简称“AAS”
  注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。
  
  要验证全等三角形，不需验证所有边及所有角也对应地相同。
  以下判定，是由三个对应的部分组成，即全等三角形可透过以下定义来判定：
  ①S.S.S. (边、边、边)：
  各三角形的三条边的长度都对应地相等的话，该两个三角形就是全等。
  ②S.A.S. (边、角、边)：
  各三角形的其中两条边的长度都对应地相等，且两条边夹着的角都对应地相等的话，该两个三角形就是全等。
  ③A.S.A. (角、边、角)：
  各三角形的其中两个角都对应地相等，且两个角夹着的边都对应地相等的话，该两个三角形就是全等。
  ④A.A.S. (角、角、边)：
  各三角形的其中两个角都对应地相等，且没有被两个角夹着的边都对应地相等的话，该两个三角形就是全等。
  ⑤R.H.S. / H.L. (直角、斜边、边)：
  各三角形的直角、斜边及另外一条边都对应地相等的话，该两个三角形就是全等。 但并非运用任何三个相等的部分便能判定三角形是否全等。以下的判定同样是运用两个三角形的三个相等的部分，但不能判定全等三角形：
  ⑥A.A.A. (角、角、角)：
  各三角形的任何三个角都对应地相等，但这并不能判定全等三角形，但则可判定相似三角形。
  ⑦A.S.S. (角、边、边)：
  各三角形的其中一个角都相等，且其余的两条边(没有夹着该角)，但这并不能判定全等三角形，除非是直角三角形。
  但若是直角三角形的话，应以R.H.S.来判定。

• 解题技巧：
  一般来说考试中线段和角相等需要证明全等。
  因此我们可以来采取逆思维的方式。
  来想要证全等，则需要什么条件:要证某某边等于某某边，那么首先要证明含有那两个边的三角形全等。
  然后把所得的等式运用（AAS/ASA/SAS/SSS/HL）证明三角形全等。
  有时还需要画辅助线帮助解题。常用的辅助线有：倍长中线，截长补短等。
  分析完毕以后要注意书写格式，在全等三角形中，如果格式不写好那么就容易出现看漏的现象。

考点名称：勾股定理的逆定理

• 勾股定理的逆定理:
  如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形。
  
  勾股定理的逆定理是判断三角形为锐角或钝角的一个简单的方法。
  若c为最长边，且a²+b²=c²，则△ABC是直角三角形。如果a²+b²>c²，则△ABC是锐角三角形。如果a²+b²<c²，则△ABC是钝角三角形。
  由于余弦定理是由勾股定理推出的，故可以用来证明其逆定理而不算循环论证。
  勾股定理的逆定理是判定三角形是不是直角三角形的重要方法。

• 勾股定理的来源：
  毕达哥拉斯树是一个基本的几何定理，传统上认为是由古希腊的毕达哥拉斯所证明。据说毕达哥拉斯证明了这个定理后，即斩了百头牛作庆祝，因此又称“百牛定理”。
  毕达哥拉斯在中国，《周髀算经》记载了勾股定理的公式与证明，相传是在商代由商高发现，故又有称之为商高定理；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，又给出了另外一个证明。法国和比利时称为驴桥定理，埃及称为埃及三角形。中国古代把直角三角形中较短的直角边叫做勾，较长的直角边叫做股，斜边叫做弦。