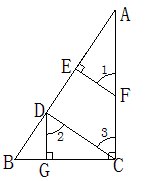
如图所示,在四边形ABCD中,AB∥CD,∠1=∠2,∠3=∠4,点E恰在AD上。(1)求证:CE⊥BE;(2)若∠D=90°,猜想CB、CD、AB之间有何数量关系?请证明你的结论。-八年级数学
题文
| 如图所示,在四边形ABCD中,AB∥CD,∠1=∠2,∠3=∠4,点E恰在AD上。 (1)求证:CE⊥BE; (2)若∠D=90°,猜想CB、CD、AB之间有何数量关系?请证明你的结论。 |
|
|
答案
| 解:(1)∵AB∥CD, ∴∠DCB+∠ABC=180°, 又∵∠1=∠2,∠3=∠4, ∴∠2+∠4=  在△BEC中, ∠CEB=180°-∠2- ∠4=90°, ∴CE⊥BE; (2)猜想:AB+CD=BC,理由如下: ∵AB∥CD,∠D=90°, ∴∠A+∠D=180°, ∴∠A=90°, ∵∠1=∠2,DE⊥CD,EF⊥CB, ∴DE=EF, 在Rt△CDE和Rt△CFE中, CE=CE,ED=EF, ∴Rt△CDE≌Rt△CFE(HL), ∴CD=CF, 同理AB=BF, ∴AB+CD= BF+CF=BC。 |
据专家权威分析,试题“如图所示,在四边形ABCD中,AB∥CD,∠1=∠2,∠3=∠4,点E恰在AD上。..”主要考查你对 垂直的判定与性质,全等三角形的性质 等考点的理解。关于这些考点的“档案”如下:
垂直的判定与性质全等三角形的性质
考点名称:垂直的判定与性质
- 垂线的定义:
两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
直线AB,CD互相垂直,记作“AB⊥CD”(或“CD⊥AB”),读作“AB垂直于CD”(或“CD垂直于AB”)。
垂线的性质:
性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连结直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
垂直的判定:垂线的定义。
考点名称:全等三角形的性质
- 全等三角形:
两个全等的三角形,而该两个三角形的三条边及三个角都对应地相等。全等三角形是几何中全等的一种。根据全等转换,两个全等三角形可以是平移、旋转、轴对称,或重叠等。当两个三角形的对应边及角都完全相对时,该两个三角形就是全等三角形。正常来说,验证两个全等三角形时都以三个相等部分来验证,最后便能得出结果。
全等三角形的对应边相等,对应角相等。
①全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
②全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
③有公共边的,公共边一定是对应边;
④有公共角的,角一定是对应角;
⑤有对顶角的,对顶角一定是对应角。 全等三角形的性质:
1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
8.全等三角形的对应角的三角函数值相等。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图所示是一人字形屋架,AB=AC,D是BC的中点,试说明:AD⊥BC。-八年级数学
下一篇:如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,求证:AD垂直平分EF。-八年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |


![如图,∠AOB=∠COD=90°,则∠AOB+∠COD[]A.大于180°B.小于180°C.等于180°D.以上答案都可能成立-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/153/2020-01-06/7f91ad736b95da9cc5086e32cb386c64.png)