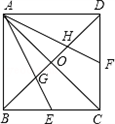
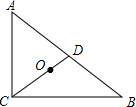
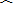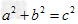给出下列四个结论:①菱形的四个顶点在同一个圆上;②正多边形都是中心对称图形;③三角形的外心到三个顶点的距离相等;④若圆心到直线上一点的距离恰好等于圆的半径,则该直线是-数学
多边形还可以分为正多边形和非正多边形。正多边形各边相等且各内角相等。
多边形也可以分为凸多边形及凹多边形,凸多边形又可称为平面多边形,凹多边形又称空间多边形
(此定理只适用于凸多边形,即平面多边形,空间多边形不适用)广义的多边形也包括五角星等图形。
多边形定理:
1、内角和定理:
n边形的内角和等于(n-2)x180°
可逆用:
·n边形的边=(内角和÷180°)+2
·过n边形一个顶点有(n-3)条对角线
·因为每个顶点和它自己及相邻的两个顶点都不能做对角线,所以n边形的每个顶点只能和n-3个其他的顶点之间做对角线,又因为每一条对角线都要连结两个顶点,所以要除以2。
n边形共有n×(n-3)÷2个对角线
· n边形过一个顶点引出所有对角线后,把多边形分成n-2个三角形
推论:
·任意凸形多边形的外角和都等于360°。
·多边形对角线的计算公式:n边形的对角线条数等于1/2·n(n-3)
·在平面内,各边相等,各内角也都相等的多边形叫做正多边形。【两个条件必须同时满足
反例:矩形(各内角相等,各边不一定相等);菱形(各边相等,各内角不一定相等)】
2、外角和定理:
n边形外角和等于n·180°-(n-2)·180°=360°
多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:若直角三角形的重心到直角顶点的距离为3厘米,则这个直角三角形的斜边长为______厘米.-数学
下一篇:Rt△ABC中,两条直角边的长分别是6cm和8cm,则Rt△ABC的外接圆的半径是______.-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |