下列说法正确的是()A.近似数0.203有两个有效数字B.15的算术平方根比4大C.多项式a-ab分解因式是a(1-b)D.函数y=-1x的图象在第一、三象限-数学
(3)连线:用平滑的曲线连接点。
当双曲线在一三象限,K>0,在每个象限内,Y随X的增大而减小。
当双曲线在二四象限,K<0,在每个象限内,Y随X的增大而增大。
常见画法当两个数相等时那么曲线呈弯月型。
过反比例函数
 (k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积
(k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积 。过反比例函数过一点,作垂线,三角形的面积为
。过反比例函数过一点,作垂线,三角形的面积为 。
。研究函数问题要透视函数的本质特征。反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积

所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。从而有k的绝对值。在解有关反比例函数的问题时,若能灵活运用反比例函数中k的几何意义,会给解题带来很多方便。
推论内容:一次函数y=x+b或y=-x+b若与反比例函数
 存在两个交点,若设2点的横坐标分别为x1,x2,那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为
存在两个交点,若设2点的横坐标分别为x1,x2,那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为

常见画法:

考点名称:算术平方根
- 概念:
若一个正数x的平方等于a,即x2=a,则这个正数x为a的算术平方根。
规定:0的算术平方根是0。
表示:a的算术平方根记为 ,读作“根号a”。
,读作“根号a”。
注:只有非负数有算术平方根,而且只有一个算术平方根。 - 平方根和算术平方根的区别与联系:
区别:
(1)定义不同:如果一个数的平方等于a,则这个数叫做a的平方根;非负数a的非负平方根叫做a的算术平方根。
(2)个数不同:一个正数有两个平方根,它们互为相反数;而一个正数的算术平方根只有一个。
(3)表示方法不同:正数a的平方根表示为± ,正数a的算术平方根表示为
,正数a的算术平方根表示为 。
。
(4)取值范围不同:正数的算术平方根一定是正数;正数的平方根一正一负,两数互为相反数。
联系:
(1)具有包含关系:平方根包含算术平方根,算术平方根是平方根的一种,是正的平方根。
(2)存在条件相同:只有非负数才有平方根和算术平方根。
(3)0的平方根,算术平方根均为0。开平方:求一个数的平方根的运算,叫做开平方。
注:
(1)平方和开平方的关系是互为逆运算;
(2)乘方是求根的途径,开平方是一种运算,是求平方根的过程;
(3)开方的方式是根号形式。 - 电脑根号的打法:
比较通用:
左手按住换档键(Alt键)不放,接着依次按41420然后松开左手,根号√ ̄就出来了。
运用Word的域命令在Word中根号:
首先按住Ctrl+F9,出现{}后,在{}内输入EQ空格\r(开方次数,根号内的表达式),最后按住Shift+F9,就会生成你所要求的根式
1.平方根
一个正数的平方根有两个,它们互为相反数。比如 9 的平方根是3,-3。而5的平方根是√5,-√5。规定,零的平方根是0。负数没有平方根。
2.算术平方根是指一个正数的正的平方根。比如 9 的算术平方根是±3。而5的算术平方根是±√5。规定,零的算术平方根是0。
算术平方根是定义在平方根基础上,因此负数没有算术平方根。
3.实数a的算术平方根记作√ ̄a,其中a≥0,根据以上定义有√ ̄a≥0。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:利用计算器计算:6×7-π=______(结果保留三位有效数字).-数学
下一篇:按四舍五入法则取近似值:2.096≈______(精确到百分位).-0.03445≈______(精确到0.001).-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

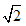
![下列结论不正确的是[]A.7.10×104精确到百位,有3个有效数字B.(a﹣2)2+|b+1|=0,则a=2,b=﹣1C.一个数的倒数等于它本身,则这个数是1D.如果一个数的绝对值等于它本身,则这个数-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/16/2019-02-21/e77ec55bf4f904dfe329ce2a0e6db3fd.png)

![四舍五入得来的近似数的有效数字是[]A.2、1、0B.2、1C.2、1、0、0、0D.3-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/16/2019-02-21/cc01152119d99d79f1a25c78c4ca93b5.png)
