题文

如图，△OAB是等腰直角三角形，∠A=90°，AO=AB．以斜边OB为直角边，按顺时针方向画等腰直角三角形OBC，再以同样的方法画等腰直角三角形OCD． （1）按照此种要求和顺序画等腰直角三角形ODE和等腰直角三角形OEF； （2）在完成（1）后，图中有位似图形吗？若有，请算出较小三角形与较大三角形的位似比．

题型：解答题  难度：中档

答案

（1）如图： （2）有，△OAB与△OEF是位似图形． 设OA=a， ∵∠A=90°，AO=AB． ∴OB= OA2+AB2 = a2+a2 = 2 a， 同理：OC= 2 ? 2 a=2a，OD= 2 ?2a=2 2 a，OE= 2 ?2 2 a=4a， ∴ OA OE = a 4a = 1 4 ， ∴较小三角形与较大三角形的位似比为1：4．

据专家权威分析，试题“如图，△OAB是等腰直角三角形，∠A=90°，AO=AB．以斜边OB为直角边，..”主要考查你对  直角三角形的性质及判定，勾股定理，位似  等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定勾股定理位似

考点名称：直角三角形的性质及判定

• 直角三角形定义：
  有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。
  

• 直角三角形性质：
  直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
  性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
  性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
  性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
  性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
  性质5:
  
  如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
  （1）（AD)2=BD·DC。
  （2）（AB)2=BD·BC。
  （3）（AC)2=CD·BC。
  性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
  在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
  性质7:如图，1/AB2+1/AC2=1/AD2
  性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
  性质9：直角三角形直角上的角平分线与斜边的交点D 则    BD:DC=AB:AC

• 直角三角形的判定方法：
  判定1：定义，有一个角为90°的三角形是直角三角形。
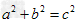  判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足，那么这个三角形就是直角三角形。（勾股定理的逆定理）。