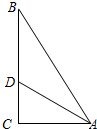
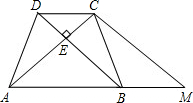
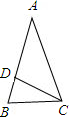
下列命题正确的有______①经过平行四边形的对角线交点的直线把平行四边形面积二等分;②⊙O中弦AB所对的圆心角为70°,点C为⊙O上一点(与A、B不重合),则∠ACB=35°;③正多边形都是-数学
区别是:
中心对称是指两个全等图形之间的相互位置关系,这两个图形关于一点对称,这个点是对称中心,两个图形关于点的对称也叫做中心对称。成中心对称的两个图形中,其中一个图形上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点的对称点,又都在这个图形上;
而中心对称图形是指一个图形本身成中心对称。中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个中心对称图形,如果把对称的部分看成是两个图形,那么它们又是关于中心对称。
也就是说:
① 中心对称图形:如果把一个图形绕某一点旋转180度后能与自身重合,这个图形是中心对称图形。
②中心对称:如果把一个图形绕某一点旋转180度后能与另一个图形重合,这两个图形成中心对称。
考点名称:圆心角,圆周角,弧和弦
圆的定义:
在同一平面内,到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度,就是圆的周长。
弧:
圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示以A,B为端点的弧记作“ ”,读作“圆弧AB”或“弧AB”。
”,读作“圆弧AB”或“弧AB”。
优弧:大于半圆的弧(多用三个字母表示);
劣弧:小于半圆的弧(多用两个字母表示)
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
弧、弦、弦心距、圆心角之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆心角:
顶点在圆心的角叫做圆心角。
圆周角:
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上,它的两边为圆的两条弦。圆心角特征识别:
①顶点是圆心;
②两条边都与圆周相交。计算公式:
①L(弧长)=n/180Xπr(n为圆心角度数,以下同);
②S(扇形面积) = n/360Xπr2;
③扇形圆心角n=(180L)/(πr)(度)。
④K=2Rsin(n/2) K=弦长;n=弦所对的圆心角,以度计。圆心角定理:
圆心角的度数等于它所对的弧的度数。
理解:(定义)
(1)等弧对等圆心角
(2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.
(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.
(4)圆心角的度数和它们对的弧的度数相等.
推论:
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明:分三种情况讨论,始终做直径COD,利用等腰三角形等腰底角相等,外角等于两内角之和来证明。
圆周角定理推论:
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中,同弧或等弧所对的圆周角相等,相等圆周角所对的弧也相等。(不在同圆或等圆中其实也相等的。注:仅限这一条。)
④半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中,圆周角相等<=>弧相等<=>弦相等。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |