如图所示,AB为⊙O的直径,P为AB延长线上一点,PD切⊙O于C,BC和AD的延长线相交于点E,且AB=AE.(1)求证:AD⊥PD;(2)若圆的半径为______,BP=1.求证:△ABE是等边三角形.(题中横线-数学-00教育-零零教育信息网
题文
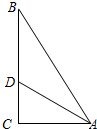
如图所示,AB为⊙O的直径,P为AB延长线上一点,PD切⊙O于C,BC和AD的延长线相交

于点E,且AB=AE.
(1)求证:AD⊥PD;
(2)若圆的半径为______,BP=1.求证:△ABE是等边三角形.(题中横线上的数字被墨迹污染了,请你填上半径的值,并证明这个题目) |
题型:解答题 难度:中档
答案

(1)证明:连接OC,
∵0C=OB,
∴∠OCB=∠OBC.
∵AB=AE,
∴∠E=∠OBC,
∴∠E=∠OCB,
∴OC∥AE.
∴∠ADC=∠OCP.
∵PD切⊙O于C,
∴∠OCP=90°.
∴∠ADC=90°.
∴AD⊥PD.
(2)若圆的半径为1时,△ABE是等边三角形.
证明:∵OB=OC=1 BP=1,
∴0C=OP.
∴∠OPC=30°,
∴∠COB=60°,
又∵OC=OB,
∴∠OBC=60°.
∵AB=AE,
∴△ABE是等边三角形. |
据专家权威分析,试题“如图所示,AB为⊙O的直径,P为AB延长线上一点,PD切⊙O于C,BC和AD..”主要考查你对 直角三角形的性质及判定,等边三角形,直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离) 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定等边三角形直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)
考点名称:直角三角形的性质及判定
考点名称:等边三角形
考点名称:直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)



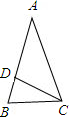
 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
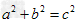 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。