题文

已知：点P为线段AB上的动点（与A、B两点不重合）．在同一平面内，把线段AP、BP分别折成△CDP、△EFP，其中∠CDP=∠EFP=90°，且D、P、F三点共线，如图所示． （1）若△CDP、△EFP均为等腰三角形，且DF=2，求AB的长； （2）若AB=12，tan∠C= 4 3 ，且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似，求四边形CDFE的面积的最小值．

题型：解答题  难度：中档

答案

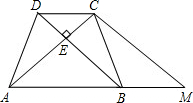
（1）设DP=x，PF=y， ∵△CDP和△EFP都是等腰直角三角形，且∠CDP=∠EFP=90°， ∴CD=DP=x，EF=PF=y，PC= 2 x，PE= 2 y． ∴AB=AP+PB=CD+DP+PC+PF+EF+PE =x+x+ 2 x+y+y+ 2 y =（2+ 2 ）（x+y）， ∵DF=2， ∴x+y=2． ∴AB=（2+ 2 ）×2=4+2 2 ； （2）连接CE． 由于tan∠C= 4 3 ，且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似，因此分两种情况考虑． ①当∠DCP=∠PEF时， 设DP=4m，PF=4n，则CD=3m，EF=3n， 根据勾股定理，可得CP=5m，PE=5n． ∵AB=CD+PC+DP+PE+EF+PF=12（m+n）=12， ∴m+n=1， ∵S四边形CDFE= 1 2 （3m+3n）（4m+4n）， =6（m+n）2 =6， 当∠DCP=∠EPF时， 设DP=4m，PF=3n，则CD=3m，EF=4n， 根据勾股定理，可得CP=5m，PE=5n． ∵AB=12（m+n）=12， ∴m+n=1． ∵m＞0，n＞0， ∴S四边形CDFE= 1 2 （3m+4n）（4m+3n） = 1 2 (12m2+25mn+12n2)= 1 2 [12(m+n)2+mn] = 1 2 （12+mn） =6+ 1 2 mn＞6， 综上所述，四边形CDFE的面积的最小值为6．

据专家权威分析，试题“已知：点P为线段AB上的动点（与A、B两点不重合）．在同一平面内，把线..”主要考查你对  直角三角形的性质及判定，勾股定理，解直角三角形  等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定勾股定理解直角三角形

考点名称：直角三角形的性质及判定

• 直角三角形定义：
  有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。