题文

如图1，已知AO是等腰Rt△ABC的角平分线，∠BAC=90°，AB=AC． （1）在图1中，∠AOC的度数为______；与线段BO相等的线段为______； （2）将图1中的△AOC绕点O顺时针旋转得到△A1OC1，如图2，连接AA1，BC1，试判断S△AOA1与S△BOC1的大小关系？并给出你的证明； （3）将图1中的△ABO绕点B顺时针旋转得到△MBN，如图3，点P为MC的中点，连接PA、PN，求证：PA=PN．

题型：解答题  难度：中档

答案

（1）∵AB=AC，AO是∠BAC的角平分线， ∴AO⊥BC， ∴∠AOC=90°，BO=OC， ∵∠BAC=90°， ∴BO=OA=OC； （2）S△AOA1=S△BOC1 ． 证明：过点O作MN⊥BC1于M，交AA1于N， ∵OB=OC1， ∴BM=C1M，∠BOM=∠C1OM， ∵∠AOB=∠A1OC1=90°， ∴∠AON+∠BOM=∠A1ON+∠C1OM=90°， ∴∠AON=∠A1ON， ∵AO=A1O， ∴ON⊥AA1， ∴∠A1NO=90°=∠OMC1， ∵在△OMC1和△A1ON中 ∠A1NO=∠C1MO ∠NA1O=∠C1OM A1O=OC1 ∴△A1ON≌△OC1M（AAS）， ∴△A1ON和△OC1M的面积相等， 同理可证△AON和△OBM的面积相等， ∴S△AOA1=S△BOC1； （3）证明：延长NP至E，使PE=NP，连接CE，AN，AE， ∵点P为MC的中点， ∴MP=CP， ∵在△PCE和△PMN中 CP=PM ∠EPC=∠MPN PE=NP ， ∴△PCE≌△PMN（SAS）， ∴CE=NM=BN，∠MNP=∠PEC， ∴CE∥MN， 设EC的延长线交BN的延长线于O， ∴∠BNM=∠BOC=90°， 又∵∠BAC=90°， ∴A、B、O、C四点共圆， ∴在四边形ABOC中，∠ACE=∠ABN， ∵在△ABN和△ACE中 AB=AC ∠ABN=∠ACE BN=CE                                            ∴△ABN≌△ACE（SAS）， ∴AN=AE，∠ABN=∠EAC， ∵∠BAC=90°=∠BAN+∠NAC=∠EAC+∠NAC=∠EAN， 即∠EAN=90°， ∵点P为NE的中点， ∴PA=PN（直角三角形斜边上中线等于斜边的一半）．

据专家权威分析，试题“如图1，已知AO是等腰Rt△ABC的角平分线，∠BAC=90°，AB=AC．（1）在图..”主要考查你对  直角三角形的性质及判定，图形旋转  等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定图形旋转

考点名称：直角三角形的性质及判定

• 直角三角形定义：
  有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。
  

• 直角三角形性质：
  直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
  性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
  性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
  性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
  性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
  性质5:
  
  如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
  （1）（AD)2=BD·DC。
  （2）（AB)2=BD·BC。
  （3）（AC)2=CD·BC。
  性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
  在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
  性质7:如图，1/AB2+1/AC2=1/AD2
  性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
  性质9：直角三角形直角上的角平分线与斜边的交点D 则    BD:DC=AB:AC

• 直角三角形的判定方法：
  判定1：定义，有一个角为90°的三角形是直角三角形。
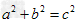  判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足，那么这个三角形就是直角三角形。（勾股定理的逆定理）。
  判定3：若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。
  判定4：两个锐角互为余角（两角相加等于90°）的三角形是直角三角形。
  判定5：若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么
  判定6：若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。
  判定7：一个三角形30°角所对的边等于这个三角形斜边的一半，则这个三角形为直角三角形。（与判定3不同，此定理用于已知斜边的三角形。）

考点名称：图形旋转