如图:在△ABC中,∠C=90°,AC=BC,D是斜边AB的中点,点E、F分别是边AC、BC上两个动点,且ED⊥DF.(1)当E、F分别在AC、BC边上移动时,并保持∠EDF=90°,DE、DF是否相等?请证明你的-数学
题文
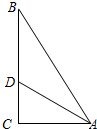
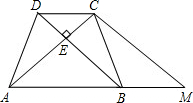
| 如图:在△ABC中,∠C=90°,AC=BC,D是斜边AB的中点,点E、F分别是边AC、BC上两个动点,且ED⊥DF. (1)当E、F分别在AC、BC边上移动时,并保持∠EDF=90°,DE、DF是否相等?请证明你的结论. (2)当E、F分别在AC、BC上移动时,并保持∠EDF=90°,S四边形DECF会随着变化吗?请证明你的结论. (3)S四边形DECF=5cm2时,求AC的长.  |


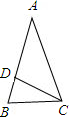
 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
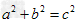 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。