题文

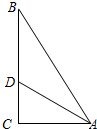
如图，已知，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=6cm；D为AC上一点（不与A、C不 重合），过D作DQ⊥AC（DQ与AB在AC的同侧）；点P从D点出发，在射线DQ上运动，连接PA、PC． （1）当PA=PC时，求出AD的长； （2）当△PAC构成等腰直角三角形时，求出AD、DP的长； （3）当△PAC构成等边三角形时，求出AD、DP的长； （4）在运动变化过程中，△CAP与△ABC能否相似？若△CAP与△ABC相似，求出此时AD与DP的长．

题型：解答题  难度：中档

答案

（1）AD= 1 2 AC= 1 2 BCtan60°=3 3 ； （2）同（1）AD=3 3 ∵∠PCD=∠DPC=45°， ∴PD=AD， ∴PD=3 3 ； （3）AD=3 3 DP=9； （4）①AD= 1 2 ×3 3 = 3 2 3 ，DP= 9 2 ； ②AD= 9 2 3 ，DP= 9 2 ．

据专家权威分析，试题“如图，已知，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=6cm；D为AC上一..”主要考查你对  直角三角形的性质及判定  等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定

考点名称：直角三角形的性质及判定

• 直角三角形定义：
  有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。
  

• 直角三角形性质：
  直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
  性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
  性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
  性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。