如图,⊙O的弦AB=10,P是弦AB所对优弧上的一个动点,tan∠APB=2,(1)若△APB为直角三角形,求PB的长;(2)若△APB为等腰三角形,求△APB的面积.-数学
题文
| 如图,⊙O的弦AB=10,P是弦AB所对优弧上的一个动点,tan∠APB=2, (1)若△APB为直角三角形,求PB的长; (2)若△APB为等腰三角形,求△APB的面积.  |
题文
| 如图,⊙O的弦AB=10,P是弦AB所对优弧上的一个动点,tan∠APB=2, (1)若△APB为直角三角形,求PB的长; (2)若△APB为等腰三角形,求△APB的面积.  |
答案
 (1)△APB是直角三角形有两种情况: 作直径AP2、BPl,连接PlA、P2B, ∴P2B=AB÷tan∠APB=5, PlB=AP2=5
所以PB的长为5或5
(2)△APB为等腰三角形时有三种情况: ①PA=PB, ∵∠AOH=∠APB,AB=10 ∴OH=
∴S△APB=
②BA=BP, ∴∠GAB=∠APB 在⊙O上取一点P4使BP4=BA,连接AP4交P1B于G 设AG=k ∵tan∠APB=2 ∴BG=2k 由勾股定理得k=2
∴S△APB=40; ③AB=AP与BA=BP情况相同 ∴S△APB=40. |
据专家权威分析,试题“如图,⊙O的弦AB=10,P是弦AB所对优弧上的一个动点,tan∠APB=2,(..”主要考查你对 直角三角形的性质及判定,等腰三角形的性质,等腰三角形的判定,勾股定理,圆心角,圆周角,弧和弦 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定等腰三角形的性质,等腰三角形的判定勾股定理圆心角,圆周角,弧和弦
考点名称:直角三角形的性质及判定
直角三角形性质:
直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质:
性质1:直角三角形两直角边a,b的平方和等于斜边c的平方。即 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
性质2:在直角三角形中,两个锐角互余。如图,若∠BAC=90°,则∠B+∠C=90°
性质3:在直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5:
如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1)(AD)2=BD·DC。
(2)(AB)2=BD·BC。
(3)(AC)2=CD·BC。
性质6:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半。
在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°。
性质7:如图,1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
性质9:直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC
直角三角形的判定方法:
判定1:定义,有一个角为90°的三角形是直角三角形。
判定2:判定定理:以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a,b,c满足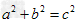 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
判定3:若一个三角形30°内角所对的边是某一边的一半,则这个三角形是以这条长边为斜边的直角三角形。
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |