已知,如图:正方形ABCD,AC是对角线,点P是AC上一点,连接PB,以PB为腰作等腰直角三角形△PBE,PE与直线AB相交于点F,连接PD,设AP=nPC.(1)如图1直接写出:PDPE=______(2)如图-数学-00教育-零零教育信息网
题文
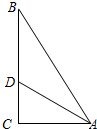
已知,如图:正方形ABCD,AC是对角线,点P是AC上一点,连接PB,以PB为腰

作等腰直角三角形△PBE,PE与直线AB相交于点F,连接PD,设AP=nPC.
(1)如图1直接写出:=______
(2)如图1当n=2时,求的值.
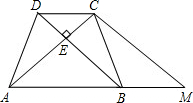
(3)如图2:当点P在AC延长线上,其它条件均不变,当n=______时,PE=5EF. |
题型:解答题 难度:中档
答案
(1);
(2)∵正方形ABCD,AC为其对角线,
∴FAP=∠BCP=45°,
∵等腰Rt△EBP,
∴∠E=∠BPF=∠PAF,
∵∠EFB=∠AFP,
∴∠EBF=∠PBC,
∵∠EBP=∠ABC=90°,
∴∠EBF=∠PBC,
∴△PFA∽△BPC,△EBP∽△ABC,
∴AP:BC=PF:BP,EP:AC=BP:BC,
∴BP:BC=PF:AP,
∴EP:AC=PF:AP,即PF:PE=AP:AC,
∵n=2,
∴AP=2PC,
∴AP:AC=2:3,
∴PF:PE=AP:AC=2:3;
(3)∵正方形ABCD,AC为其对角线,
∴∠BAC=∠BCA=45°,
∵等腰直角三角形EBP,
∴∠BEP=∠BPE=45°,
∴△EBP∽△ABC,
∴EP:AC=BP:BC,
∴∠FBE=∠FPA,
∵∠ABC=∠EBP=90°,
∴∠FBE=∠PBC,
∴∠PBC=∠FPA,
∴△PBC∽△FPA,
∴AP:BC=PF:BP,
∴BP:BC=PF:AP,
∵BP:BC=PE:AC,
∴PF:AP=PE:AC,即PE:PF=AC:AP,
∵PE=5EF,
∴PE:PF=5:6,
∴AC:AP=5:6,
∴AP:PC=6:1,
∵AP=nPC,
∴n=6,
∴当n=6时,PE=5EF.
故答案为,6. |
据专家权威分析,试题“已知,如图:正方形ABCD,AC是对角线,点P是AC上一点,连接PB,以..”主要考查你对 直角三角形的性质及判定,正方形,正方形的性质,正方形的判定 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定正方形,正方形的性质,正方形的判定
考点名称:直角三角形的性质及判定
考点名称:正方形,正方形的性质,正方形的判定


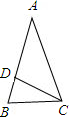
 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
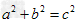 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。