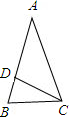
如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点E为线段AB上任意一点(E不与B重合),以CE为斜边作等腰Rt△CDE,连接AD,下列结论:①∠BCE=∠ACD;②∠BCE=∠AED;③BE=AD;④AD∥BC;⑤四边形-数学
题文
| 如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点E为线段AB上任意一点(E不与B重合),以CE为斜边作等腰Rt△CDE,连接AD,下列结论: ①∠BCE=∠ACD;②∠BCE=∠AED;③BE=AD;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
其中正确的结论有( )个.
 |
答案
| ∵△ABC、△DCE都是等腰Rt△, ∴AB=AC=
∠B=∠ACB=∠DEC=∠DCE=45°; ①∵∠ACB=∠DCE=45°, ∴∠ACB-∠ACE=∠DCE-∠ACE; 即∠ECB=∠DCA;故①正确; ②∵∠AED+∠DEC+∠BEC=180°,∠DEC=45°, ∴∠AED+∠BEC=135°, 又∵∠BCE+∠BEC=180°-∠B=180°-45°=135°, ∴∠AED=∠BCE,故此选项正确; ③∵
∴
由①知∠ECB=∠DCA, ∴△BEC∽△ADC; ∴
∴BE≠AD,故此选项错误; ④∵△BEC∽△ADC; ∴∠DAC=∠B=45°; ∴∠DAC=∠BCA=45°, 即AD∥BC,故④正确; ⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大; △ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大; 由④的△BEC∽△ADC知:当AD最长时,BE也最长; 故梯形ABCD面积最大时,E、A重合,此时EC=AC=
故S梯形ABCD=
|