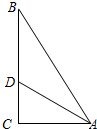
如图1,点C将线段AB分成两部分,如果ACAB=BCAC,那么称点C为线段AB的黄金分割点.(1)某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分-数学
题文
如图1,点C将线段AB分成两部分,如果
(1)某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
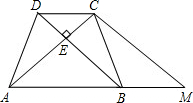
 问题.试在图3的梯形中画出至少五条黄金分割线,并说明理由. (2)类似“黄金分割线”得“黄金分割面”定义:截面a将一个体积为V的图形分成体积为V  1、V2的两个图形,且 1、V2的两个图形,且
问题:如图4,长方体ABCD-EFGH中,T是线段AB上的黄金分割点,证明经过T点且平行于平面BCGF的截面QRST是长方体的黄金分割面. |
答案
| (1)如图,先在梯形的中位线EF上找一个黄金分割点G,过点G作一条直线L交AD于点M,交BC于N,则MN就是梯形的黄金分割线. ∵EG:EF=GF:EG, ∴EG×h:EF×h=GF×h:EG×h, ∵S梯形ABNM=EG×h,S梯形MNCD=GF×h,S梯形ABCD=EF×h(h是梯形的高), ∴S梯形ABNM:S梯形ABCD=S梯形NMCD:S梯形ABNM, ∵直线L是过G的任意一条与AD,BC都相交的直线, ∴符合题意的黄金分割线有无穷多条. (2)∵AT:AB=TB:AT, ∴S矩形QRST=S矩形BCGF, ∵AT×S矩形QRST:AB×S矩形BCGF=TB×S矩形ADHE:AT×S矩形QRST, 即截面QRST将体积为V的长方体,分成左右两块体积分别是V1,V2, ∴V1:V=V2:V1, ∴截面QRST是长方体的黄金分割面.  |
据专家权威分析,试题“如图1,点C将线段AB分成两部分,如果ACAB=BCAC,那么称点C为线段..”主要考查你对 直角三角形的性质及判定 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定
考点名称:直角三角形的性质及判定
- 直角三角形定义:
有一个角为90°的三角形,叫做直角三角形。直角三角形可用Rt△表示,如直角三角形ABC写作Rt△ABC。 直角三角形性质:
直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质:
性质1:直角三角形两直角边a,b的平方和等于斜边c的平方。即 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
性质2:在直角三角形中,两个锐角互余。如图,若∠BAC=90°,则∠B+∠C=90°
性质3:在直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5:
如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1)(AD)2=BD·DC。
(2)(AB)2=BD·BC。
(3)(AC)2=CD·BC。
性质6:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半。
在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°。
性质7:如图,1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
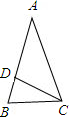
性质9:直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC直角三角形的判定方法:
判定1:定义,有一个角为90°的三角形是直角三角形。
判定2:判定定理:以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a,b,c满足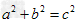 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
判定3:若一个三角形30°内角所对的边是某一边的一半,则这个三角形是以这条长边为斜边的直角三角形。
判定4:两个锐角互为余角(两角相加等于90°)的三角形是直角三角形。
判定5:若两直线相交且它们的斜率之积互为负倒数,则两直线互相垂直。那么
判定6:若在一个三角形中一边上的中线等于其所在边的一半,那么这个三角形为直角三角形。
判定7:一个三角形30°角所对的边等于这个三角形斜边的一半,则这个三角形为直角三角形。(与判定3不同,此定理用于已知斜边的三角形。)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |