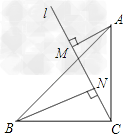
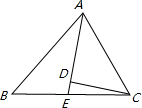
已知:如图,C为半圆O上一点,,过点C作直径AB的垂线CP,弦AE分别交PC、CB于点D、F。(1)求证:AD=CD;(2)若DF=,∠CAE=30°,求阴影部分的面积.。-九年级数学
(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.
(4)圆心角的度数和它们对的弧的度数相等.
推论:
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等
与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明:分三种情况讨论,始终做直径COD,利用等腰三角形等腰底角相等,外角等于两内角之和来证明。
圆周角定理推论:
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中,同弧或等弧所对的圆周角相等,相等圆周角所对的弧也相等。(不在同圆或等圆中其实也相等的。注:仅限这一条。)
④半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中,圆周角相等<=>弧相等<=>弦相等。
考点名称:组合图形面积
- 组合图形:
是由几种基本图形(三角形、平行四边形、正方形、梯形、圆)组合而成的较复杂的平面图形。
求组合图形的面积就是对组合图形进行分割或添补转化为我们学过的三角形、平行四边形、梯形、圆的面积来求解。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图,点A的坐标是(1,1),若点B在x轴上,且△ABO是等腰三角形,则点B的坐标不可能是[]A.(2,0)B.(,0)C.(,0)D.(1,0)-九年级数学
下一篇:如图,△ABC,点D、E分别在AB、AC上,给出5个论断:①CD⊥AB,②BE⊥AC,③AE=CE,④∠ABE=30°,⑤CD=BE。(1)如果论断①、②、③、④都成立,那么论断⑤一定成立吗?(2)从论断①、②、③、④中选-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |