在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10cm，CD=4cm。等腰直角三角形PMN的斜边MN=10cm，A点与N点重合，MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角三角形PMN沿AB所在-九年级数学-00教育-零零教育信息网

在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10cm，CD=4cm。等腰直角三角形PMN的斜边MN=10cm，A点与N点重合，MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角三角形PMN沿AB所在-九年级数学

首页 > 考试 > 数学 > 初中数学 > 等腰三角形的性质，等腰三角形的判定/2020-05-20 / 加入收藏 / 阅读 [打印]

题文

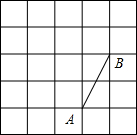
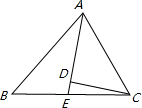
在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10cm，CD=4cm。等腰直角三角形PMN的斜边MN=10cm，A点与N点重合，MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角三角形PMN沿AB所在直线以1cm/s的速度向右移动，直到点N与点B重合为止．
（1）等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分的形状由_____________变化为__________；
（2）设当等腰直角三角形PMN移动x (s) 时，等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为
y(cm²)：
     ①当x=6 s时，则y的值是_________ cm²；（直接写出答案，不必写出过程）
     ②求x为何值时，y=4 cm²；（要求写出过程）
     ③当x=_________ s时，y=15 cm²．（要求写出过程）

题型：解答题难度：偏难

答案

（1）等腰直角三角形；等腰梯形
（2）等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分图形的形状可分为以下两种情况：

   ① 9
   ② 当时，重叠部分的形状为等腰直角三角形EAN（如图①）
     此时AN=x（cm），过点E作EH⊥AB于点H，则EH平分AN，
    ∴EH=AN=x，
   则y=S_△ANE=AN·EH=x·x=x²∴x²=4         解得x₁= 4 ，x₂= -4（不合题意，舍去）
    ∴x=4
    ∴ 当x=4（s）时，等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积是4 cm²。
   ③解：当6<x≤10时，重叠部分的形状是等腰梯形ANED（如图②）
   此时AN=x（cm）   ∵ ∠PNM=∠B=45°，∴EN∥BC
   ∵ CE∥BN，∴四边形ENBC是平行四边形，CE=BN=10-x，DE=4-(10-x)=x-6；
   过点D作DF⊥AB于F，过点C作CG⊥AB于G，则AF=BG，DF=AF=(10-4)=3，
    ∴ y=S梯形ANED=(DE+AN)·DF= (x-6+x)×3=3x-9
   ∴3x-9=15，解得x=8

据专家权威分析，试题“在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10cm，CD=4cm。等腰直角三..”主要考查你对等腰三角形的性质，等腰三角形的判定，一元二次方程的应用，梯形，梯形的中位线等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定一元二次方程的应用梯形，梯形的中位线

考点名称：等腰三角形的性质，等腰三角形的判定

定义：
有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：一元二次方程的应用

建立一元二次方程模型进行求解，把得到的答案带回实际问题中检验是否合理，来解决实际问题，如打折、营销、增长率问题等。
列一元二次次方程组解应用题的一般步骤:
可概括为“审、设、列、解、答”五步，即：
（1）审：是指读懂题意，弄清题意，明确哪些是已知量，哪些是未知量以及它们之间的关系；
（2）设：是指设未知数；
（3）列：就是列方程，这是非常重要的一步，一般先找出能够表达应用题全部含义的一个等量关系，然后列代数式表示等量关系中的各个量，就得到含有未知数的等式，即方程；
（4）解：解这个方程，求出两个未知数的值；
（5）答：在对求出的方程的解做出是否合理判断的基础上，写出答案。
提示：
①列方程解应用题时，要善于将普通语言化为数学语言，审题时，要特别注意关键词语，如“多、少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等，此外，还要掌握一些常用的公式或特殊的等量关系，如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等。