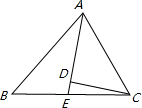
在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N。(1)如图1,当点M在AB边上时,连接BN。①求证:△ABN≌△ADN;②若∠ABC=60°,AM=4,∠ABN=α,求点M到-九年级数学
题文
| 在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N。 |
|
|
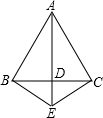
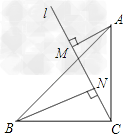
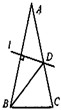
| (1)如图1,当点M在AB边上时,连接BN。 ①求证:△ABN≌△ADN; ②若∠ABC=60°,AM=4,∠ABN=α,求点M到AD的距离及tanα的值; (2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12),试问:x为何值时,△ADN为等腰三角形。 |
答案
| 解:(1)①证明:∵四边形ABCD是菱形 ∴AB=AD,∠1=∠2 又∵AN=AN ∴△ABN≌△ADN ②作MH⊥DA交DA的延长线于点H,由AD∥BC,得∠MAH=∠ABC=60°, 在Rt△AMH中,MH=AM·sin60°=4×sin60°=2  , ,∴点M到AD的距离为2  , ,易求AH=2,则DH=6+2=8 在Rt△DMH中,tan∠MDH=  , ,由①知,∠MDH=∠ABN=α,故tanα=  ; ; |
 |
| (2)∵∠ABC=90°, ∴菱形ABCD是正方形,此时,∠CAD=45°, 下面分三种情形: Ⅰ)若ND=NA,则∠ADN=∠NAD=45° 此时,点M恰好与点B重合,得x=6; Ⅱ)若DN=DA,则∠DNA=∠DAN=45° 此时,点M恰好与点C重合,得x=12; Ⅲ)若AN=AD=6,则∠1=∠2, 由AD∥BC,得∠1=∠4, 又∠2=∠3, ∴∠3=∠4,从而CM=CN, 易求AC=6  , ,∴CM=CN=AC-AN=6  -6, -6,故x=12-CM=12-(6  -6)=18-6 -6)=18-6 , ,综上所述:当x=6或12或18-6  时,△ADN是等腰三角形。 时,△ADN是等腰三角形。 |
 |
据专家权威分析,试题“在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连..”主要考查你对 等腰三角形的性质,等腰三角形的判定,三角形全等的判定,解直角三角形 等考点的理解。关于这些考点的“档案”如下:
等腰三角形的性质,等腰三角形的判定三角形全等的判定解直角三角形
考点名称:等腰三角形的性质,等腰三角形的判定
- 定义:
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。 等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
考点名称:三角形全等的判定
三角形全等判定定理:
1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了
三角形具有稳定性的原因。
2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)
5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边,直角边”) 所以:SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
注意:在全等的判定中,没有AAA和SSA,这两种情况都不能唯一确定三角形的形状。三角形全等的判定公理及推论:
(1)“边角边”简称“SAS”
(2)“角边角”简称“ASA”
(3)“边边边”简称“SSS”
(4)“角角边”简称“AAS”
注意:在全等的判定中,没有AAA和SSA,这两种情况都不能唯一确定三角形的形状。
要验证全等三角形,不需验证所有边及所有角也对应地相同。
以下判定,是由三个对应的部分组成,即全等三角形可透过以下定义来判定:
①S.S.S. (边、边、边):
各三角形的三条边的长度都对应地相等的话,该两个三角形就是全等。
②S.A.S. (边、角、边):
各三角形的其中两条边的长度都对应地相等,且两条边夹着的角都对应地相等的话,该两个三角形就是全等。
③A.S.A. (角、边、角):
各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等的话,该两个三角形就是全等。
④A.A.S. (角、角、边):
各三角形的其中两个角都对应地相等,且没有被两个角夹着的边都对应地相等的话,该两个三角形就是全等。
⑤R.H.S. / H.L. (直角、斜边、边):
各三角形的直角、斜边及另外一条边都对应地相等的话,该两个三角形就是全等。 但并非运用任何三个相等的部分便能判定三角形是否全等。以下的判定同样是运用两个三角形的三个相等的部分,但不能判定全等三角形:
⑥A.A.A. (角、角、角):
各三角形的任何三个角都对应地相等,但这并不能判定全等三角形,但则可判定相似三角形。
⑦A.S.S. (角、边、边):
各三角形的其中一个角都相等,且其余的两条边(没有夹着该角),但这并不能判定全等三角形,除非是直角三角形。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |