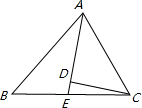
下列说法中,正确的说法有①对角线相等的平行四边形是矩形;②等腰三角形中有两边长分别为3和2,则周长为8;③依次连接等腰梯形各边中点所得的四边形是菱形;④点P(3,-5)到x轴的-八年级数学
众数:作为一组数据的代表,可靠性也比较差,因为它也只利用了部分数据。。在一组数据中,如果个别数据有很大的变动,且某个数据出现的次数最多,此时用该数据(即众数)表示这组数据的“集中趋势”就比较适合。
中位数:
①将数据按大小顺序排列;
②当数据个数为奇数时,中间的那个数据就是中位数;
当数据个数为偶数时,居于中间的两个数据的平均数才是中位数。
众数:找出频数最多的数据,若几个数据频数最多且相同,此时众数就是这几个数据。
考点名称:矩形,矩形的性质,矩形的判定
- 矩形:
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。 矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形- 矩形的判定:
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。 - 黄金矩形:
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。如希腊的巴特农神庙等。
考点名称:菱形,菱形的性质,菱形的判定
- 菱形的定义:
在一个平面内,有一组邻边相等的平行四边形是菱形。 菱形的性质:
①菱形具有平行四边形的一切性质;
②菱形的对角线互相垂直且平分,并且每一条对角线平分一组对角;
③菱形的四条边都相等;
④菱形既是轴对称图形(两条对称轴分别是其两条对角线所在的直线),也是中心对称图形(对称中心是其重心,即两对角线的交点);
⑤在有一个角是60°角的菱形中,较短的对角线等于边长,较长的对角线是较短的对角线的根号3倍。菱形的判定:
在同一平面内,
(1)定义:有一组邻边相等的平行四边形是菱形
(2)定理1:四边都相等的四边形是菱形
(3)定理2:对角线互相垂直的平行四边形是菱形
菱形是在平行四边形的前提下定义的,首先它是平行四边形,而且是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而增加了一些特殊的性质和判定方法。
菱形的面积:S菱形=底边长×高=两条对角线乘积的一半。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图,若等腰△ABC的腰长AB=10cm,AB的垂直平分线交另一腰AC于D,△BCD的周长为16cm,则底边BC是()。-八年级数学
下一篇:在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是[]A.25°B.25°或40°C.40°或30°D.50°-八年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |