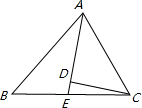
如图,△ABC中,AD⊥BC于D,∠B=2∠C.(1)求证:DC=BD+AB;(2)若设CD=a、BD=b、AB=c,试说明方程x2﹣ax+bc=0有两个不相等的实数根;(3)若方程x2﹣ax+bc=0的一根是另一根的2倍,试判断-九年级数学
题文
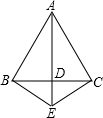
| 如图,△ABC中,AD⊥BC于D,∠B=2∠C. (1)求证:DC=BD+AB; (2)若设CD=a、BD=b、AB=c,试说明方程x2﹣ax+bc=0有两个不相等的实数根; (3)若方程x2﹣ax+bc=0的一根是另一根的2倍,试判断△ABC的形状. |
 |
答案
| (1)证明:在BC上取点E,使BD=DE, ∵AD⊥BC, ∴AB=AE, ∴∠AEB=∠ABC=2∠C, ∵∠C=∠EAC ∴EC=EA=AB, ∴CD=DE+EC=BD+AB (2)解:由(1)得: ∵a2﹣4bc=(b+c)2﹣4bc=(b﹣c)2又c>b,即c≠b, ∴(b﹣c)2>0, ∴方程x2﹣ax+bc=0有两个不相等的实数根. (3)解:设方程的两根为k,2k,代入得k2﹣ak+bc=0 ①及4k2﹣2ak+bc=0②, 由②﹣4×①得k=  ,代入①得( ,代入①得( )2﹣a )2﹣a +bc=0, +bc=0,化简得9bc=2a2,又∵a2=(b+c)2代入得2b2﹣5bc+2c2=0, (2b﹣c)(b﹣2c)=0, ∵b<c, ∴c=2b ∵AD⊥BC, ∴∠B=60°, ∴∠C=30°, ∴∠BAC=90°,∴△ABC为直角三角形. |
 |
据专家权威分析,试题“如图,△ABC中,AD⊥BC于D,∠B=2∠C.(1)求证:DC=BD+AB;(2)若设CD=a..”主要考查你对 等腰三角形的性质,等腰三角形的判定,一元二次方程根与系数的关系,一元二次方程根的判别式 等考点的理解。关于这些考点的“档案”如下:
等腰三角形的性质,等腰三角形的判定一元二次方程根与系数的关系一元二次方程根的判别式
考点名称:等腰三角形的性质,等腰三角形的判定
- 定义:
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。 等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
考点名称:一元二次方程根与系数的关系
- 一元二次方程根与系数的关系:
如果方程 的两个实数根是
的两个实数根是 那么
那么 ,
, 。
。
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。 一元二次方程根与系数关系的推论:
1.如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p , x1`x2=q
2.以两个数x1、x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1x2=0
提示:
①运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式,以便正确确定a、b、c的值。
②有推论1可知,对于二次项系数为1的一元二次方程,他的两根之和等于一次项系数的相反数,两根之积等于常数项。
③推论2可以看作推论1的逆定理,利用推论2可以直接求出以两个数x1、x2为根的一元二次方程(二次项系数是1)是x2-(x1+x2)x+x1x2=0
考点名称:一元二次方程根的判别式
- 根的判别式:
一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac。
定理1 ax2+bx+c=0(a≠0)中,△>0 方程有两个不等实数根;
方程有两个不等实数根;
定理2 ax2+bx+c=0(a≠0)中,△=0 方程有两个相等实数根;
方程有两个相等实数根;
定理3 ax2+bx+c=0(a≠0)中,△<0 方程没有实数根。
方程没有实数根。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |