题文

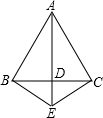
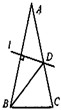
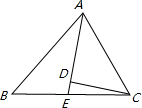
已知等腰△ABC中，AB=AC，AD平分∠BAC交BC于D点，在线段AD上任取一点P（A点除外），过P点作 EF∥AB，分别交AC，BC于E，F点，作PM∥AC，交AB于M点，连接ME． （1）求证：四边形AEPM为菱形； （2）当P点在何处时，菱形AEPM的面积为四边形EFBM面积的一半？

题型：解答题  难度：中档

答案

（1）证明：∵EF∥AB，PM∥AC， ∴四边形AEPM为平行四边形． ∵AB=AC，AD平分∠CAB， ∴∠CAD=∠BAD， ∵AD⊥BC（三线合一的性质）， ∵∠BAD=∠EPA， ∴∠CAD=∠EPA， ∵EA=EP， ∴四边形AEPM为菱形． （2） P为EF中点时，S菱形AEPM= 1 2 S四边形EFBM ∵四边形AEPM为菱形， ∴AD⊥EM， ∵AD⊥BC， ∴EM∥BC， 又EF∥AB， ∴四边形EFBM为平行四边形． 作EN⊥AB于N，则S菱形AEPM=EP?EN= 1 2 EF?EN= 1 2 S四边形EFBM．

据专家权威分析，试题“已知等腰△ABC中，AB=AC，AD平分∠BAC交BC于D点，在线段AD上任取一..”主要考查你对  等腰三角形的性质，等腰三角形的判定，平行四边形的性质，菱形，菱形的性质，菱形的判定  等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定平行四边形的性质菱形，菱形的性质，菱形的判定

考点名称：等腰三角形的性质，等腰三角形的判定

• 定义：
  有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

• 等腰三角形的性质：
  1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
  2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
  3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
  4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
  5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
  6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
  7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
  8.等腰三角形中腰的平方等于高的平方加底的一半的平方
  9.等腰三角形中腰大于高
  10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

• 等腰三角形的判定：
  1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
  2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
  3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：平行四边形的性质

• 平行四边形的概念：
  两组对边分别平行的四边形叫做平行四边形。
  平行四边形用符号“□ABCD，如平行四边形ABCD记作“□ABCD”，读作ABCD”。
  ①平行四边形属于平面图形。
  ②平行四边形属于四边形。
  ③平行四边形中还包括特殊的平行四边形：矩形，正方形和菱形等。
  ④平行四边形属于中心对称图形。

• 平行四边形的性质：
  主要性质
  （矩形、菱形、正方形都是特殊的平行四边形。）
  （1）如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。
  （简述为“平行四边形的两组对边分别相等”）
  （2）如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等。
  （简述为“平行四边形的两组对角分别相等”）
  （3）如果一个四边形是平行四边形，那么这个四边形的邻角互补
  （简述为“平行四边形的邻角互补”）
  （4）夹在两条平行线间的平行线段相等。
  （5）如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分。
  （简述为“平行四边形的对角线互相平分”）
  （6）连接任意四边形各边的中点所得图形是平行四边形。(推论）
  （7）平行四边形的面积等于底和高的积。（可视为矩形）
  （8）过平行四边形对角线交点的直线，将平行四边形分成全等的两部分图形。
  （9）平行四边形是中心对称图形，对称中心是两对角线的交点.
  （10）平行四边形不是轴对称图形，矩形和菱形是轴对称图形。
  注：正方形，矩形以及菱形也是一种特殊的平行四边形，三者具有平行四边形的性质。
  
  （11）平行四边形ABCD中（如图）E为AB的中点，则AC和DE互相三等分，一般地，若E为AB上靠近A的n等分点，则AC和DE互相(n+1)等分。
  （12）平行四边形ABCD中，AC、BD是平行四边形ABCD的对角线，则各四边的平方和等于对角线的平方和。
  （13）平行四边形对角线把平行四边形面积分成四等分。
  （14）平行四边形中，两条在不同对边上的高所组成的夹角，较小的角等于平行四边形中较小的角，较大的角等于平行四边形中较大的角。
  （15）平行四边形中,一个角的顶点向他对角的两边所做的高，与这个角的两边组成的夹角相等。

考点名称：菱形，菱形的性质，菱形的判定

• 菱形的定义:
  在一个平面内，有一组邻边相等的平行四边形是菱形。

• 菱形的性质:
  ①菱形具有平行四边形的一切性质；
  ②菱形的对角线互相垂直且平分，并且每一条对角线平分一组对角；
  ③菱形的四条边都相等；
  ④菱形既是轴对称图形（两条对称轴分别是其两条对角线所在的直线），也是中心对称图形（对称中心是其重心，即两对角线的交点）；
  ⑤在有一个角是60°角的菱形中，较短的对角线等于边长，较长的对角线是较短的对角线的根号3倍。

• 菱形的判定:
  在同一平面内，
  （1）定义：有一组邻边相等的平行四边形是菱形
  （2）定理1：四边都相等的四边形是菱形
  （3）定理2：对角线互相垂直的平行四边形是菱形