题文

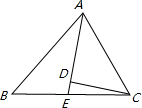
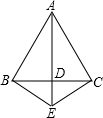
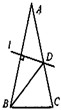
某小区现有一块等腰直角三角形形状的绿地，腰长为100米，直角顶点为A．小区物业管委会准备把它分割成面积相等的两块，有如下的分割方法： 方法一：在底边BC上找一点D，连接AD作为分割线； 方法二：在腰AC上找一点D，连接BD作为分割线； 方法三：在腰AB上找一点D，作DE∥BC，交AC于点E，DE作为分割线； 方法四：以顶点A为圆心，AD为半径作弧，交AB于点D，交AC于点E，弧DE作为分割线． 这些分割方法中分割线最短的是（　　） A．方法一 B．方法二 C．方法三 D．方法四

题型：单选题  难度：偏易

答案

根据等腰直角三角形的性质， 方法一中AD= 100 2 =50 2 ； 方法二中BD= 1002+502 =50 5 ； 方法三中，△ADE∽△ABC，有DE2：BC2=S△ADE：S△ABC=1：2， ∵腰长为100米， ∴BC=100 2 ， ∴DE=100； 方法四中，S△ABC= 1 2 ×100×100=5000， ∴扇形的面积= 5000 2 =2500= 1 4 ×AD2π， ∴AD= 100 π ， ∴ DE = 90×2π× 100 π 360 =50 π ． 则方法一中的分割线最短． 故选A．

据专家权威分析，试题“某小区现有一块等腰直角三角形形状的绿地，腰长为100米，直角顶点..”主要考查你对  等腰三角形的性质，等腰三角形的判定，勾股定理，弧长的计算 ，扇形面积的计算   等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定勾股定理弧长的计算 扇形面积的计算

考点名称：等腰三角形的性质，等腰三角形的判定