题文

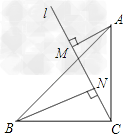
如图，在锐角△ABC中，BA=BC，点O是边AB上的一个动点（不与点A、B重合），以O为圆心，OA为半径的圆交边AC于点M，过点M作⊙O的切线MN交BC于点N． （1）当OA=OB时，求证：MN⊥BC； （2）分别判断OA＜OB、OA＞OB时，上述结论是否成立，请选择一种情况，说明理由．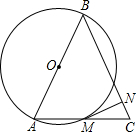

题型：解答题  难度：中档

答案

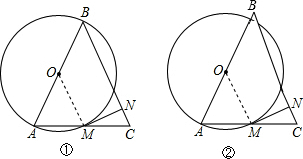
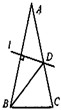
（1）证明：如图①，连接OM，则OM⊥MN； ∵在△OAM中，OA=OM， ∴∠A=∠OMA； ∵在△BAC中，BA=BC， ∴∠A=∠C， ∴∠OMA=∠C， ∴OM∥BC， ∴MN⊥BC； （2）当OA＜OB时，成立；当OA＞OB时，也成立． 以OA＜OB为例进行说明，如图②，OA＜OB，连接OM； ∵在△OAM中，OA=OM， ∴∠A=∠OMA； ∵在△BAC中，BA=BC， ∴∠A=∠C， ∴∠OMA=∠C， ∴OM∥BC， ∴MN⊥BC．

据专家权威分析，试题“如图，在锐角△ABC中，BA=BC，点O是边AB上的一个动点（不与点A、B重..”主要考查你对  等腰三角形的性质，等腰三角形的判定，圆心角，圆周角，弧和弦，直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）  等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定圆心角，圆周角，弧和弦直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

考点名称：等腰三角形的性质，等腰三角形的判定

• 定义：
  有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

• 等腰三角形的性质：
  1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
  2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
  3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
  4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
  5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
  6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
  7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
  8.等腰三角形中腰的平方等于高的平方加底的一半的平方
  9.等腰三角形中腰大于高
  10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

• 等腰三角形的判定：
  1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
  2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
  3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：圆心角，圆周角，弧和弦

• 圆的定义:
  在同一平面内，到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度，就是圆的周长。
  
  弧：
  圆上任意两点间的部分叫做圆弧，简称弧。
  弧用符号“⌒”表示以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。
  优弧：大于半圆的弧（多用三个字母表示）；
  劣弧：小于半圆的弧（多用两个字母表示）
  圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。 
   弧、弦、弦心距、圆心角之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。
  推论：在同圆或等圆中，如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。
  
  圆心角：
  顶点在圆心的角叫做圆心角。
  
  圆周角：
  顶点在圆上，并且两边都和圆相交的角叫做圆周角。
  圆周角的顶点在圆上，它的两边为圆的两条弦。

• 圆心角特征识别:
  ①顶点是圆心；
  ②两条边都与圆周相交。

  计算公式:
  ①L(弧长)=n/180Xπr（n为圆心角度数，以下同）；
  ②S(扇形面积) = n/360Xπr²；
  ③扇形圆心角n=（180L）/（πr）（度）。
  ④K=2Rsin(n/2) K=弦长；n=弦所对的圆心角，以度计。

  圆心角定理:
  圆心角的度数等于它所对的弧的度数。
  理解：(定义）
  （1）等弧对等圆心角
  （2）把顶点在圆心的周角等分成360份时，每一份的圆心角是1°的角．
  （3）因为在同圆中相等的圆心角所对的弧相等，所以整个圆也被等分成360份，这时，把每一份这样得到的弧叫做1°的弧．
  （4）圆心角的度数和它们对的弧的度数相等．
  推论：
  在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等

  与圆周角关系:
  在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
  定理证明：分三种情况讨论，始终做直径COD，利用等腰三角形等腰底角相等，外角等于两内角之和来证明。
  
  圆周角定理推论：
  圆周角定理:在同圆或等圆中，同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
  ①圆周角度数定理：圆周角的度数等于它所对的弧的度数的一半。
  ②同圆或等圆中，圆周角等于它所对的弧上的圆心角的一半。
  ③同圆或等圆中，同弧或等弧所对的圆周角相等，相等圆周角所对的弧也相等。（不在同圆或等圆中其实也相等的。注：仅限这一条。）
  ④半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径。
  ⑤圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。
  ⑥在同圆或等圆中，圆周角相等<=>弧相等<=>弦相等。

考点名称：直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

• 直线与圆的位置关系:
  直线与圆的位置关系有三种：直线与圆相交，直线与圆相切，直线与圆相离。
  （1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点AB与⊙O相交，d<r；
  （2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，这个唯一的公共点叫做切点。AB与⊙O相切，d=r。
  （3）相离：直线和圆没有公共点时，叫做直线和圆相离,AB与圆O相离，d>r。（d为圆心到直线的距离）

• 直线与圆的三种位置关系的判定与性质：
  （1）数量法：通过比较圆心O到直线距离d与圆半径的大小关系来判定，
  如果⊙O的半径为r，圆心O到直线l的距离为d，则有：
  直线l与⊙O相交d<r；
  直线l与⊙O相切d=r；