题文

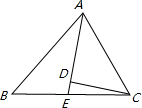
如图，在矩形ABCD中，点E在AD上，EC平分∠BED． （1）试判断△BEC是否为等腰三角形，请说明理由？ （2）若AB=1，∠ABE=45°，求BC的长． （3）在原图中画△FCE，使它与△BEC关于CE的中点O成中心对称，此时四边形BCFE是什么特殊平行四边形，请说明理由．

题型：解答题  难度：中档

答案

（1）∵AD∥BC， ∴∠DEC=∠BCE， ∵∠DEC=∠BEC， ∴∠BEC=∠BCE， ∴△BCE是等腰三角形． （2）∵在Rt△ABE中，∠ABE=45°， ∴∠AEB=∠ABE=45°， ∴AB=AE=1． ∴BE= 2 ， ∴BC= 2 ． （3）如图，∵△FCE与△BEC关于CE的中点O成中心对称， ∴OB=OF，OE=OC， ∴四边形BCFE是平行四边形， 又∵BC=BE， ∴四边形BCFE是菱形．

据专家权威分析，试题“如图，在矩形ABCD中，点E在AD上，EC平分∠BED．（1）试判断△BEC是否为..”主要考查你对  等腰三角形的性质，等腰三角形的判定，矩形，矩形的性质，矩形的判定，菱形，菱形的性质，菱形的判定，中心对称  等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定矩形，矩形的性质，矩形的判定菱形，菱形的性质，菱形的判定中心对称

考点名称：等腰三角形的性质，等腰三角形的判定

• 定义：
  有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

• 等腰三角形的性质：
  1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
  2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
  3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
  4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
  5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
  6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
  7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
  8.等腰三角形中腰的平方等于高的平方加底的一半的平方
  9.等腰三角形中腰大于高
  10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

• 等腰三角形的判定：
  1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
  2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
  3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：矩形，矩形的性质，矩形的判定

• 矩形:
  是一种平面图形，矩形的四个角都是直角，同时矩形的对角线相等，而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。

• 矩形的性质：
  1．矩形的4个内角都是直角；
  2．矩形的对角线相等且互相平分；
  3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等；
  4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线），它至少有两条对称轴。对称中心是对角线的交点。
  5．矩形是特殊的平行四边形，矩形具有平行四边形的所有性质
  6.顺次连接矩形各边中点得到的四边形是菱形

• 矩形的判定：
  ①定义：有一个角是直角的平行四边形是矩形
  ②定理1：有三个角是直角的四边形是矩形
  ③定理2：对角线相等的平行四边形是矩形
  ④对角线互相平分且相等的四边形是矩形
  矩形的面积：S_矩形=长×宽=ab。

• 黄金矩形:
  宽与长的比是（√5-1）/2（约为0.618）的矩形叫做黄金矩形。
  黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。如希腊的巴特农神庙等。

考点名称：菱形，菱形的性质，菱形的判定

• 菱形的定义:
  在一个平面内，有一组邻边相等的平行四边形是菱形。

• 菱形的性质:
  ①菱形具有平行四边形的一切性质；
  ②菱形的对角线互相垂直且平分，并且每一条对角线平分一组对角；
  ③菱形的四条边都相等；
  ④菱形既是轴对称图形（两条对称轴分别是其两条对角线所在的直线），也是中心对称图形（对称中心是其重心，即两对角线的交点）；
  ⑤在有一个角是60°角的菱形中，较短的对角线等于边长，较长的对角线是较短的对角线的根号3倍。

• 菱形的判定:
  在同一平面内，
  （1）定义：有一组邻边相等的平行四边形是菱形
  （2）定理1：四边都相等的四边形是菱形
  （3）定理2：对角线互相垂直的平行四边形是菱形
  菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。
  菱形的面积：S_菱形=底边长×高=两条对角线乘积的一半。

考点名称：中心对称

• 中心对称的定义：
  把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么说这两个图形关于这个点中心对称，这个点叫做对称中心。
  中心对称图形的定义：
  在平面内，一个图形绕着某一个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。

• 中心对称的性质：
  ①关于中心对称的两个图形是全等形。
  ②关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
  ③关于中心对称的两个图形，对应线段平行（或在同一直线上）且相等。
  
  中心对称的判定：
  如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。 

• 中心对称与中心对称图形的联系: 
  中心对称和中心对称图形是两个不同而又紧密联系的概念。