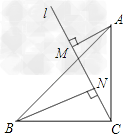
在△ABC中,∠BAC=90°,AB=AC,点D是线段BC上的一个动点(不与点B重合).DE⊥BE于E,∠EBA=12∠ACB,DE与AB相交于点F.(1)当点D与点C重合时(如图1),探究线段BE与FD的数量关系,并加-数学
题文
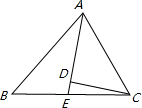
在△ABC中,∠BAC=90°,AB=AC,点D是线段BC上的一个动点(不与点B重合).DE⊥BE于E,∠EBA=
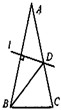
(1)当点D与点C重合时(如图1),探究线段BE与FD的数量关系,并加以证明; (2)当点D与点C不重合时(如图2),试判断(1)中的猜想是否仍然成立,请说明理由.  |