题文

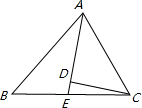
已知，梯形ABCD中，AD∥BC，M为BC上一点，若将△ABM绕点M顺时针旋转一定角度，恰好与 △CDM重合． （1）在上述旋转过程中，旋转角为图中的哪个角？ 请在横线上直接填出答案：______； （2）小明发现△MAD为等腰三角形，请你帮他说明理由； （3）本题中，你还有什么发现？请写出一条，并说明理由．

题型：解答题  难度：中档

答案

（1）∠BMD； （2）∵AD∥BC， ∴∠BMA=∠MAD，∠DMC=∠MDA， 由旋转知∠BMA=∠DMC， ∴∠MAD=∠MDA， ∴MA=MD，即△MAD为等腰三角形； （3）M为BC的中点； ∵△ABM绕点M顺时针旋转一定角度，恰好与△CDM重合， ∴BM=CM， ∴M为BC的中点．

据专家权威分析，试题“已知，梯形ABCD中，AD∥BC，M为BC上一点，若将△ABM绕点M顺时针旋转..”主要考查你对  等腰三角形的性质，等腰三角形的判定，图形旋转  等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定图形旋转

考点名称：等腰三角形的性质，等腰三角形的判定

• 定义：
  有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

• 等腰三角形的性质：
  1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
  2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
  3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
  4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
  5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
  6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
  7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
  8.等腰三角形中腰的平方等于高的平方加底的一半的平方
  9.等腰三角形中腰大于高
  10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

• 等腰三角形的判定：
  1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
  2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
  3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：图形旋转

• 定义：
  在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。
  图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。

• 图形旋转性质：
  （1）对应点到旋转中心的距离相等。
  （2）对应点与旋转中心所连线段的夹角等于旋转角。
  旋转对称中心
  把一个图形绕着一个点旋转一定的角度后，与原来的图形相吻合，这种图形叫做 旋转对称图形，这个定点叫做 旋转对称中心，旋转的角度叫做 旋转角。（旋转角大于0°小于360°）