题文

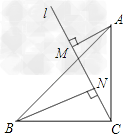
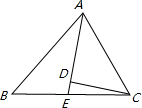
如图，在△ABC中，AB=AC，DE=EC，DH∥BC，EF∥AB，HE的延长线与BC的延长线相交于 点M，点G在BC上，且∠1=∠2，不添加辅助线，解答下列问题： （1）找出一个等腰三角形；（不包括△ABC） （2）找出三对相似三角形；（不包括全等三角形） （3）找出两对全等三角形，并选出一对进行证明．

题型：解答题  难度：中档

答案

（1）∵AB=AC， ∴∠B=∠ACB， ∵DH∥BC， ∴∠AHD=∠B，∠ADH=∠ACB， ∴∠AHD=∠ADH， ∴△AHD是等腰三角形； ∵DH∥BC， ∴∠2=∠M又∠1=∠2， ∴∠1=∠M， ∴△EGM是等腰三角形； ∵AB=AC， ∴∠B=ACB， ∵EF∥AB，∠B=∠EFC， ∴∠ACB=∠EFC ∴△EFC是等腰三角形； （2）△AHD∽△ABC，△EFC∽△ABC，△EFM∽△HBM，△AHD∽△EFC，△BMH∽△CGE（写出其中三对即可）．（3分） ∵HD∥BC， ∴△AHD∽△ABC， ∵EF∥AB， ∴△EFC∽△ABC，△EFM∽△HBM； （3）△DHE≌△FGE，△DHE≌△CME，△FGE≌△CME，△EGC≌△EMF（写出其中两对即可）（2分） 选择△DHE≌△CME． 证明：∵DH∥CM， ∴∠2=∠M， 又∵∠DEH=∠CEM，DE=EC， ∴△DHE≌△CME（2分） ∵HD∥BC，EF∥AB， ∴∠2=∠M，∠B=EFC又∠B=∠ACB，∠1=∠2， ∴∠1=∠M，∠EFC=∠ECF， ∴∠EFG=∠ECM， ∴△EFG≌△ECM． 说明：选任何一对全等三角形，只要证明正确均得分．

据专家权威分析，试题“如图，在△ABC中，AB=AC，DE=EC，DH∥BC，EF∥AB，HE的延长线与BC的..”主要考查你对  等腰三角形的性质，等腰三角形的判定，三角形全等的判定，相似三角形的性质  等考点的理解。关于这些考点的“档案”如下：

等腰三角形的性质，等腰三角形的判定三角形全等的判定相似三角形的性质

考点名称：等腰三角形的性质，等腰三角形的判定

• 定义：
  有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

• 等腰三角形的性质：
  1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
  2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
  3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
  4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
  5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
  6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
  7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
  8.等腰三角形中腰的平方等于高的平方加底的一半的平方
  9.等腰三角形中腰大于高
  10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

• 等腰三角形的判定：
  1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
  2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
  3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：三角形全等的判定

• 三角形全等判定定理：
  1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”)，这一条也说明了
  三角形具有稳定性的原因。
  2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
  3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
  4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)
  5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边，直角边”) 所以：SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
  注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。

• 三角形全等的判定公理及推论：
  (1)“边角边”简称“SAS”
  (2)“角边角”简称“ASA”
  (3)“边边边”简称“SSS”
  (4)“角角边”简称“AAS”
  注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。
  
  要验证全等三角形，不需验证所有边及所有角也对应地相同。
  以下判定，是由三个对应的部分组成，即全等三角形可透过以下定义来判定：
  ①S.S.S. (边、边、边)：
  各三角形的三条边的长度都对应地相等的话，该两个三角形就是全等。
  ②S.A.S. (边、角、边)：
  各三角形的其中两条边的长度都对应地相等，且两条边夹着的角都对应地相等的话，该两个三角形就是全等。
  ③A.S.A. (角、边、角)：
  各三角形的其中两个角都对应地相等，且两个角夹着的边都对应地相等的话，该两个三角形就是全等。
  ④A.A.S. (角、角、边)：
  各三角形的其中两个角都对应地相等，且没有被两个角夹着的边都对应地相等的话，该两个三角形就是全等。
  ⑤R.H.S. / H.L. (直角、斜边、边)：
  各三角形的直角、斜边及另外一条边都对应地相等的话，该两个三角形就是全等。 但并非运用任何三个相等的部分便能判定三角形是否全等。以下的判定同样是运用两个三角形的三个相等的部分，但不能判定全等三角形：
  ⑥A.A.A. (角、角、角)：
  各三角形的任何三个角都对应地相等，但这并不能判定全等三角形，但则可判定相似三角形。
  ⑦A.S.S. (角、边、边)：
  各三角形的其中一个角都相等，且其余的两条边(没有夹着该角)，但这并不能判定全等三角形，除非是直角三角形。
  但若是直角三角形的话，应以R.H.S.来判定。

• 解题技巧：
  一般来说考试中线段和角相等需要证明全等。
  因此我们可以来采取逆思维的方式。
  来想要证全等，则需要什么条件:要证某某边等于某某边，那么首先要证明含有那两个边的三角形全等。
  然后把所得的等式运用（AAS/ASA/SAS/SSS/HL）证明三角形全等。
  有时还需要画辅助线帮助解题。常用的辅助线有：倍长中线，截长补短等。
  分析完毕以后要注意书写格式，在全等三角形中，如果格式不写好那么就容易出现看漏的现象。

考点名称：相似三角形的性质

• 相似三角形性质定理：
  (1)相似三角形的对应角相等。
  (2)相似三角形的对应边成比例。
  (3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。
  (4)相似三角形的周长比等于相似比。
  (5)相似三角形的面积比等于相似比的平方。
  (6)相似三角形内切圆、外接圆直径比和周长比都和相似比相同，内切圆、外接圆面积比是相似比的平方
  (7)若a/b =b/c，即b2=ac，b叫做a,c的比例中项
  (8)c/d=a/b 等同于ad=bc.
  (9)不必是在同一平面内的三角形里
  ①相似三角形对应角相等，对应边成比例.
  ②相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比.
  ③相似三角形周长的比等于相似比

  定理推论：
  推论一：顶角或底角相等的两个等腰三角形相似。
  推论二：腰和底对应成比例的两个等腰三角形相似。
  推论三：有一个锐角相等的两个直角三角形相似。
  推论四：直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
  推论五：如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。