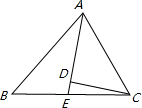
下列说法不正确的是()A.角平分线上的点到这个角两条边的距离相等B.线段的垂直平分线上的点到这条线段的两个端点的距离相等C.圆有无数条对称轴D.等腰三角形的对称轴是底角的平-数学
③有两个公共点的叫相交。两圆圆心之间的距离叫做圆心距。
设两圆的半径分别为R和r,且R〉r,圆心距为P,则结论:外离P>R+r;外切P=R+r;内含P<R-r;
内切P=R-r;相交R-r<P<R+r。
圆的计算公式:
1.圆的周长C=2πr=或C=πd
2.圆的面积S=πr2
3.扇形弧长L=圆心角(弧度制)× r = n°πr/180°(n为圆心角)
4.扇形面积S=nπ r2/360=Lr/2(L为扇形的弧长)
5.圆的直径 d=2r
6.圆锥侧面积 S=πrl(l为母线长)
7.圆锥底面半径 r=n°/360°L(L为母线长)(r为底面半径)
圆的方程:
1、圆的标准方程:在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是
(x-a)2+(y-b)2=r2。
特别地,以原点为圆心,半径为r(r>0)的圆的标准方程为x2+y2=r2。
2、圆的一般方程:方程x2+y2+Dx+Ey+F=0可变形为(x+D/2)2+(y+E/2)2=(D2+E2-4F)/4.故有:
①当D2+E2-4F>0时,方程表示以(-D/2,-E/2)为圆心,以(√D2+E2-4F)/2为半径的圆;
②当D2+E2-4F=0时,方程表示一个点(-D/2,-E/2);
③当D2+E2-4F<0时,方程不表示任何图形。
3、圆的参数方程:以点O(a,b)为圆心,以r为半径的圆的参数方程是 x=a+r*cosθ, y=b+r*sinθ, (其中θ为参数)
圆的端点式:若已知两点A(a1,b1),B(a2,b2),则以线段AB为直径的圆的方程为 (x-a1)(x-a2)+(y-b1)(y-b2)=0
圆的离心率e=0,在圆上任意一点的曲率半径都是r。
经过圆x2+y2=r2上一点M(a0,b0)的切线方程为 a0·x+b0·y=r2
在圆(x2+y2=r2)外一点M(a0,b0)引该圆的两条切线,且两切点为A,B,则A,B两点所在直线的方程也为 a0·x+b0·y=r2。
圆的历史:
圆形,是一个看来简单,实际上是十分奇妙的形状。古代人最早是从太阳、阴历十五的月亮得到圆的概念的。在一万八千年前的山顶洞人曾经在兽牙、砾石和石珠上钻孔,那些孔有的就很圆。到了陶器时代,许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。当人们开始纺线,又制出了圆形的石纺锤或陶纺锤。古代人还发现搬运圆的木头时滚着走比较省劲。后来他们在搬运重物的时候,就把几段圆木垫在大树、大石头下面滚着走,这样当然比扛着走省劲得多。
约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆型的木盘。大约在4000多年前,人们将圆的木盘固定在木架下,这就成了最初的车子。
会作圆,但不一定就懂得圆的性质。古代埃及人就认为:圆,是神赐给人的神圣图形。一直到两千多年前我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。意思是说:圆有一个圆心,圆心到圆周的长都相等。这个定义比希腊数学家欧几里得(约公元前330-前275年)给圆下定义要早100年。
任意一个圆的周长与它直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际运用中一般只取它的近似值,即π≈3.14.如果用C表示圆的周长:C=πd或C=2πr.《周髀算经》上说"周三径一",把圆周率看成3,但是这只是一个近似值。美索不达来亚人在作第一个轮子的时候,也只知道圆周率是3。魏晋时期的刘徽于公元263年给《九章算术》作注时,发现"周三径一"只是圆内接正六边形周长和直径的比值。他创立了割圆术,认为圆内接正多连形边数无限增加时,周长就越逼近圆周长。他算到圆内接正3072边形的圆周率,π= 3927/1250。刘徽把极限的概念运用于解决实际的数学问题之中,这在世界数学史上也是一项重大的成就。祖冲之(公元429-500年)在前人的计算基础上继续推算,求出圆周率在3.1415926与3.1415927之间,是世界上最早的七位小数精确值,他还用两个分数值来表示圆周率:22/7称为约率,355/113称为密率。 在欧洲,直到1000年后的十六世纪,德国人鄂图(公元1573年)和安托尼兹才得到这个数值。现在有了电子计算机,圆周率已经算到了小数点后六十万亿位小数了。
考点名称:角平分线的性质
角平分线:
三角形的一个角的平分线与这个角的对边相交,连结这个角的顶点和与对边交点的线段叫做三角形的角平分线(也叫三角形的内角平分线)。由定义可知,三角形的角平分线是一条线段。由于三角形有三个内角,所以三角形有三条角平分线。三角形的角平分线交点一定在三角形内部。角平方线定理:
①角平分线上的任意一点,到角两边的距离相等。垂直于两边为最短距离。
②角平分线能得到相同的两个角,都等于该角的一半。
③三角形三条角平分线相交于一点,并且这一点到三边的距离相等。
④三角形的三个角的角平分线相交于一点,这个点称为内心 ,即以此点为圆心可以在三角形内部画一个内切圆。
逆定理:
在角的内部,到角两边的距离相等的点在角平分线上。- 角平分线作法:
在角AOB中,画角平分线
方法一:
1.以点O为圆心,以任意长为半径画弧,两弧交角AOB两边于点M,N。
2.分别以点M,N为圆心,以大于1/2MN的长度为半径画弧,两弧交于点P。
3.作射线OP。
则射线OP为角AOB的角平分线。
当然,角平分线的作法有很多种。下面再提供一种尺规作图的方法供参考。
方法二:
1.在两边OA、OB上分别截取OM、OA和ON、OB,且使得OM=ON,OA=OB;
2.连接AN与BM,他们相交于点P;
3.作射线OP。
则射线OP为角AOB的角平分线。
考点名称:垂直平分线的性质
- 垂直平分线的概念:
垂直于一条线段并且平分这条线段的直线,叫做这条线段的垂直平分线(中垂线)。
如图:直线MN即为线段AB的垂直平分线。
- 垂直平分线的性质:
1.垂直平分线垂直且平分其所在线段。
2.垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
3.如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。
4.三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相 等。
(此时以外心为圆心,外心到顶点的长度为半径,所作的圆为此三角形的外接圆。)
判定:
①利用定义;
②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(即线段垂直平分线可以看成到线段两端点距离相等的点的集合) 尺规作法:(用圆规作图)
1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。
2、分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线。得到两个交点(两交点交与线段的异侧)。
3、连接这两个交点。
原理:等腰三角形的高垂直平分底边。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |