已知:如下图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其B,C,D点的坐标分别为(1,2),(1,1),(3,1)。(1)求E点和A点的坐标;(2)试以点P(0,2)为位似中心,作出相-九年级数学
题文
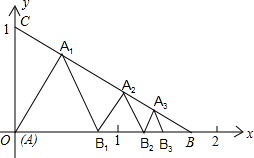
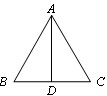
| 已知:如下图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其B,C,D点的坐标分别为(1,2),(1,1),(3,1)。 |
|
|
| (1)求E点和A点的坐标; (2)试以点P(0,2)为位似中心,作出相似比为3的位似图形A1B1C1D1E1,并写出各对应点的坐标; (3)将图形A1B1C1D1E1向右平移4个单位长度后,再作关于x轴的对称图形,得到图形A2B2C2D2E2,这时它的各顶点坐标分别是多少? |
答案
解:(1) ; ;(2)  ,B1(3,2),C1(3,-1),D1(9,-1),E1(9,2),图“略”。 ,B1(3,2),C1(3,-1),D1(9,-1),E1(9,2),图“略”。(3)  ,B2(7,-2),C2(7,1),D2(13,1),E2(13,-2)。 ,B2(7,-2),C2(7,1),D2(13,1),E2(13,-2)。 |
据专家权威分析,试题“已知:如下图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其..”主要考查你对 等边三角形,轴对称,矩形,矩形的性质,矩形的判定,位似,平移 等考点的理解。关于这些考点的“档案”如下:
等边三角形轴对称矩形,矩形的性质,矩形的判定位似平移
考点名称:等边三角形
- 等边三角形定义:
三条边都相等的三角形叫做等边三角形,“等边三角形”也被称为“正三角形”。是特殊的等腰三角形。
如果一个三角形满足下列任意一条,则它必满足另一条,三边相等或三角相等的三角形叫做等边三角形:
1.三边长度相等;
2.三个内角度数均为60度;
3.一个内角为60度的等腰三角形。 性质:
①等边三角形是锐角三角形,等边三角形的内角都相等,且均为60°。
②等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一)
③等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线 或对角的平分线所在的直线。
④等边三角形重心、内心、外心、垂心重合于一点,称为等边三角形的中心。(四心合一)
⑤等边三角形内任意一点到三边的距离之和为定值(等于其高)判定方法:
①三边相等的三角形是等边三角形(定义)
②三个内角都相等(为60度)的三角形是等边三角形
③有一个角是60度的等腰三角形是等边三角形
④ 两个内角为60度的三角形是等边三角形
说明:可首先考虑判断三角形是等腰三角形。
等边三角形的性质与判定理解:
首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。等比三角形的尺规做法:
可以利用尺规作图的方式画出正三角形,其作法相当简单:先用尺画出一条任意长度的线段(这条线段的长度决定等边三角形的边长),再分别以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原来线段的两个端点画线段,则这二条线段和原来线段即构成一正三角形。
考点名称:轴对称
- 轴对称的定义:
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。轴对称和轴对称图形的特性是相同的,对应点到对称轴的距离都是相等的。 轴对称的性质:
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等;
(3)关于某直线对称的两个图形是全等图形。轴对称的判定:
如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
这样就得到了以下性质:
1.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
2.类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
3.线段的垂直平分线上的点与这条线段的两个端点的距离相等。
4.对称轴是到线段两端距离相等的点的集合。轴对称作用:
可以通过对称轴的一边从而画出另一边。
可以通过画对称轴得出的两个图形全等。
扩展到轴对称的应用以及函数图像的意义。轴对称的应用:
关于平面直角坐标系的X,Y对称意义
如果在坐标系中,点A与点B关于直线X对称,那么点A的横坐标不变,纵坐标为相反数。
相反的,如果有两点关于直线Y对称,那么点A的横坐标为相反数,纵坐标不变。关于二次函数图像的对称轴公式(也叫做轴对称公式 )
设二次函数的解析式是 y=ax2+bx+c
则二次函数的对称轴为直线 x=-b/2a,顶点横坐标为 -b/2a,顶点纵坐标为 (4ac-b2)/4a在几何证题、解题时,如果是轴对称图形,则经常要添设对称轴以便充分利用轴对称图形的性质。
譬如,等腰三角形经常添设顶角平分线;
矩形和等腰梯形问题经常添设对边中点连线和两底中点连线;
正方形,菱形问题经常添设对角线等等。
另外,如果遇到的图形不是轴对称图形,则常选择某直线为对称轴,补添为轴对称图形,
或将轴一侧的图形通过翻折反射到另一侧,以实现条件的相对集中。
考点名称:矩形,矩形的性质,矩形的判定
- 矩形:
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。 矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形- 矩形的判定:
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。 - 黄金矩形:
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |


![如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点P是直线上异于A,B的一个动点,且满足∠CPD=30°,则[]A.点P一定在射线BE上B.点P一定在线段AB上C.点P可以在射线A-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/2df74dbaef06dd0b4b9202993c0acb78.gif)
![如图,一边长为8cm的正三角形木板ABC,在水平桌面上绕点B顺时针旋转至A′BC′的位置时,顶点C从开始到结束所经过的路径长为(点A、B、C′在同一直线上)[]A.16B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/db2fcc20ff63ed308b2e0babcde2f13d.gif)