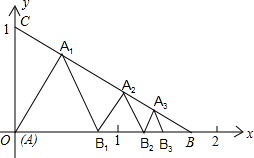
如图,△ABE和△ACD都是等边三角形,△EAC旋转后能与△ABD重合,EC与BD相交于点F。(1)试说明△AEC≌△ABD;(2)求∠DFC的度数。-七年级数学
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
8.全等三角形的对应角的三角函数值相等。
考点名称:三角形全等的判定
三角形全等判定定理:
1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了
三角形具有稳定性的原因。
2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)
5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边,直角边”) 所以:SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
注意:在全等的判定中,没有AAA和SSA,这两种情况都不能唯一确定三角形的形状。三角形全等的判定公理及推论:
(1)“边角边”简称“SAS”
(2)“角边角”简称“ASA”
(3)“边边边”简称“SSS”
(4)“角角边”简称“AAS”
注意:在全等的判定中,没有AAA和SSA,这两种情况都不能唯一确定三角形的形状。
要验证全等三角形,不需验证所有边及所有角也对应地相同。
以下判定,是由三个对应的部分组成,即全等三角形可透过以下定义来判定:
①S.S.S. (边、边、边):
各三角形的三条边的长度都对应地相等的话,该两个三角形就是全等。
②S.A.S. (边、角、边):
各三角形的其中两条边的长度都对应地相等,且两条边夹着的角都对应地相等的话,该两个三角形就是全等。
③A.S.A. (角、边、角):
各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等的话,该两个三角形就是全等。
④A.A.S. (角、角、边):
各三角形的其中两个角都对应地相等,且没有被两个角夹着的边都对应地相等的话,该两个三角形就是全等。
⑤R.H.S. / H.L. (直角、斜边、边):
各三角形的直角、斜边及另外一条边都对应地相等的话,该两个三角形就是全等。 但并非运用任何三个相等的部分便能判定三角形是否全等。以下的判定同样是运用两个三角形的三个相等的部分,但不能判定全等三角形:
⑥A.A.A. (角、角、角):
各三角形的任何三个角都对应地相等,但这并不能判定全等三角形,但则可判定相似三角形。
⑦A.S.S. (角、边、边):
各三角形的其中一个角都相等,且其余的两条边(没有夹着该角),但这并不能判定全等三角形,除非是直角三角形。
但若是直角三角形的话,应以R.H.S.来判定。解题技巧:
一般来说考试中线段和角相等需要证明全等。
因此我们可以来采取逆思维的方式。
来想要证全等,则需要什么条件:要证某某边等于某某边,那么首先要证明含有那两个边的三角形全等。
然后把所得的等式运用(AAS/ASA/SAS/SSS/HL)证明三角形全等。
有时还需要画辅助线帮助解题。常用的辅助线有:倍长中线,截长补短等。
分析完毕以后要注意书写格式,在全等三角形中,如果格式不写好那么就容易出现看漏的现象。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

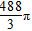
![如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点P是直线上异于A,B的一个动点,且满足∠CPD=30°,则[]A.点P一定在射线BE上B.点P一定在线段AB上C.点P可以在射线A-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/2df74dbaef06dd0b4b9202993c0acb78.gif)
![如图,一边长为8cm的正三角形木板ABC,在水平桌面上绕点B顺时针旋转至A′BC′的位置时,顶点C从开始到结束所经过的路径长为(点A、B、C′在同一直线上)[]A.16B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/db2fcc20ff63ed308b2e0babcde2f13d.gif)