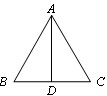
已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF、AC交于点N.(1)如图①,当AD⊥BC时,请说明DF⊥AC的理由;(2)如图②,当点D在BC上移动时,以AD为边再向左作等边△AD-数学
题文
| 已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF、AC交于点N. (1)如图①,当AD⊥BC时,请说明DF⊥AC的理由; (2)如图②,当点D在BC上移动时,以AD为边再向左作等边△ADE,DE、AB交于M,试问线段AM和AN有什么数量关系?请说明你的理由; (3)在(2)的基础上,若等边△ABC的边长为2,直接写出DM+DN的最小值.  |


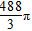
![如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点P是直线上异于A,B的一个动点,且满足∠CPD=30°,则[]A.点P一定在射线BE上B.点P一定在线段AB上C.点P可以在射线A-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/2df74dbaef06dd0b4b9202993c0acb78.gif)
![如图,一边长为8cm的正三角形木板ABC,在水平桌面上绕点B顺时针旋转至A′BC′的位置时,顶点C从开始到结束所经过的路径长为(点A、B、C′在同一直线上)[]A.16B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/db2fcc20ff63ed308b2e0babcde2f13d.gif)