如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立,请证明,若不成立-数学
题文
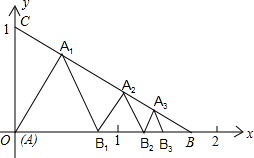
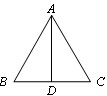
如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形. (1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立,请证明,若不成立,请说明理由; (2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由. |
答案
| (1)CD=BE.理由如下:(1分) ∵△ABC和△ADE为等边三角形, ∴AB=AC,AE=AD,∠BAC=∠EAD=60°, ∵∠BAE=∠BAC-∠EAC=60°-∠EAC, ∠DAC=∠DAE-∠EAC=60°-∠EAC, ∴∠BAE=∠DAC,(3分) ∴△DAC≌△EAB(SAS), ∴CD=BE.(4分) (2)△AMN是等边三角形.理由如下:(5分) ∵△ABE≌△ACD, ∴∠ABE=∠ACD ∵M、N分别是BE、CD的中点, ∴BM=
∵AB=AC,∠ABE=∠ACD, ∴△ABM≌△ACN. ∴AM=AN,∠MAB=∠NAC.(6分) ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°, ∴△AMN是等边三角形.(7分) 设AD=a,则AB=2a. ∵AD=AE=DE,AB=AC, ∴CE=DE. ∵△ADE为等边三角形, ∴∠DEC=120°,∠ADE=60°, ∴∠EDC=∠ECD=30°, ∴∠ADC=90°.(8分) ∴在Rt△ADC中,AD=a,∠ACD=30°, ∴CD=
∵N为DC中点, ∴DN=
∴AN=
∵△ADE,△ABC,△AMN为等边三角形, ∴S△ADE:S△ABC:S△AMN=a2:(2a)2:(
解法二:△AMN是等边三角形.理由如下:(5分) ∵△ABE≌△ACD,M、N分别是BE、CD的中点, ∴AM=AN,NC=MB. ∵AB=AC, ∴△ABM≌△ACN, ∴∠MAB=∠NAC, ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°, ∴△AMN是等边三角形,(7分) 设AD=a,则AD=AE=DE=a,AB=BC=AC=2a, 易证BE⊥AC, ∴BE= |

![如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点P是直线上异于A,B的一个动点,且满足∠CPD=30°,则[]A.点P一定在射线BE上B.点P一定在线段AB上C.点P可以在射线A-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/2df74dbaef06dd0b4b9202993c0acb78.gif)
![如图,一边长为8cm的正三角形木板ABC,在水平桌面上绕点B顺时针旋转至A′BC′的位置时,顶点C从开始到结束所经过的路径长为(点A、B、C′在同一直线上)[]A.16B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/162/2020-05-20/db2fcc20ff63ed308b2e0babcde2f13d.gif)