小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作:(1)操作一:如上图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE。①如果AC=6cm,BC=8cm,试-八年级数学
题文
| 小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作: |
|
|
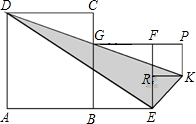
| (1)操作一:如上图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE。 ①如果AC=6cm,BC=8cm,试求△ACD的周长。 ②如果∠CAD:∠BAD=4:7,求∠B的度数。 (2)操作二:如图,小丽拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm,BC=8cm,你能求出CD的长吗? |
|
|
| (3)操作三:如图,小丽又拿出另一张Rt△ABC纸片,将纸片折叠,折痕CD⊥AB。你能证明:BC2+AD2=AC2+BD2 吗? |
|
|
答案
| 解:(1)①由对称性可得AD=BD, ∵△ACD的周长=AC+CD+AD ∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(㎝); ②设∠CAD=4x ,∠BAD=7x 由题意得方程:7x+7x+4x=90 解之得:x=5 所以∠B=35; (2)设CD= x,则BD=8-x,DE=x 由题意可得方程  解之得:x=3 所以CD=3㎝; (3)在Rt△BCD中,由勾股定理可得  在Rt△ACD中,由勾股定理可得 AD2+CD2= AC2 ∴BC2+AD2=BD2+CD2+AD2= AC2+BD2 ; |
据专家权威分析,试题“小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作..”主要考查你对 三角形的周长和面积,轴对称,勾股定理 等考点的理解。关于这些考点的“档案”如下:
三角形的周长和面积轴对称勾股定理
考点名称:三角形的周长和面积
- 三角形的概念:
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。 - 三角形的分类:
(1)三角形按边的关系分类如下: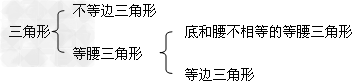 ;
;
(2)三角形按角的关系分类如下:
把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。 - 三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
考点名称:轴对称
- 轴对称的定义:
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。轴对称和轴对称图形的特性是相同的,对应点到对称轴的距离都是相等的。 轴对称的性质:
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等;
(3)关于某直线对称的两个图形是全等图形。轴对称的判定:
如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
这样就得到了以下性质:
1.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
2.类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
3.线段的垂直平分线上的点与这条线段的两个端点的距离相等。
4.对称轴是到线段两端距离相等的点的集合。轴对称作用:
可以通过对称轴的一边从而画出另一边。
可以通过画对称轴得出的两个图形全等。
扩展到轴对称的应用以及函数图像的意义。轴对称的应用:
关于平面直角坐标系的X,Y对称意义
如果在坐标系中,点A与点B关于直线X对称,那么点A的横坐标不变,纵坐标为相反数。
相反的,如果有两点关于直线Y对称,那么点A的横坐标为相反数,纵坐标不变。关于二次函数图像的对称轴公式(也叫做轴对称公式 )
设二次函数的解析式是 y=ax2+bx+c
则二次函数的对称轴为直线 x=-b/2a,顶点横坐标为 -b/2a,顶点纵坐标为 (4ac-b2)/4a在几何证题、解题时,如果是轴对称图形,则经常要添设对称轴以便充分利用轴对称图形的性质。
譬如,等腰三角形经常添设顶角平分线;
矩形和等腰梯形问题经常添设对边中点连线和两底中点连线;
正方形,菱形问题经常添设对角线等等。
另外,如果遇到的图形不是轴对称图形,则常选择某直线为对称轴,补添为轴对称图形,
或将轴一侧的图形通过翻折反射到另一侧,以实现条件的相对集中。
考点名称:勾股定理
- 勾股定理:
直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 。
。
勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。 - 定理作用
⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
⑵勾股定理导致不可通约量的发现,从而深刻揭示了数与量的区别,即所谓“无理数"与有理数的差别,这就是所谓第一次数学危机。
⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
⑷勾股定理中的公式是第一个不定方程,也是最早得出完整解答的不定方程,它一方面引导到各式各样的不定方程,包括著名的费尔马大定理,另一方面也为不定方程的解题程序树立了一个范式。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |




![如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是[]A.2B.3C.4D.5-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/163/2020-05-20/facf2a6d7f4f4e42254e6c9026b6dc15.png)